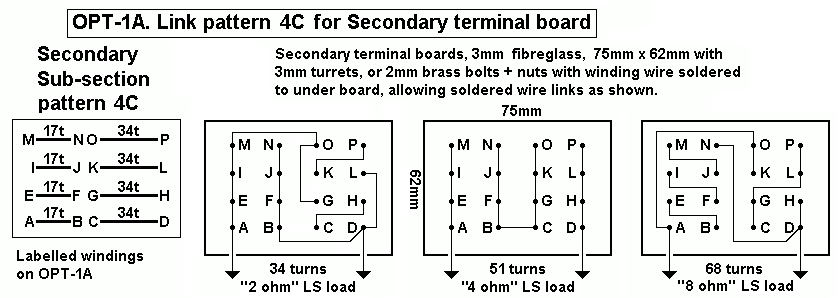
| TABLE 2. OPT Power |
Total Pri layers |
Primary and
Secondary layer distribution. |
P&S section pattern |
| 0 to 7W | 10p to 24p | S - 10p~24p - S | 2S + 1P |
| 7W to 15W | 10p to 20p | S - 5p~10p - S - 5p~10p - S | 3S + 2P |
| 7W to 15W | 10p to 20p | 2p~4p - S - 4p~8p - S - 4p~8p - S - 2p~4p | 3S + 4P |
| TABLE 3. OPT Power |
Total Pri layers |
Primary and Secondary layer distribution. |
P&S section pattern |
| 15W to 35W | 12p | 2p - S - 4p - S - 4p - S - 2p | 3S + 4P |
| 12p | S - 4p - S - 4p - S - 4p - S | 4S + 3P | |
| 14p | 2p - S - 3p - S - 4p - S - 3p - S - 2p | 3S + 4P | |
| 14p | S - 5p - S - 4p - S - 5p - S | 4S + 3P | |
| 16p | 3p - S - 5p - S - 5p - S - 3p | 3S + 4P | |
| 16p | S - 4p - S - 4p - S - 4p - S - 4p - S | 5S + 4P | |
| 16p | 2p - S - 4p - S - 4p - S - 4p - S - 2p | 4S + 5P | |
| 18p | 3p - S - 6p - S - 6p - S - 3p | 3S + 4P | |
| 18p | S - 4p - S - 5p - S - 5p - S - 4p - S | 5S + 4P | |
| 20p | 3p - S - 7p - S - 7p - S - 3p | 4S + 3P | |
| 20p | S - 5p - S - 5p - S - 5p - S - 5p - S | 5S + 4P | |
| 20p | 2p - S - 5p - S - 6p - S - 5p - S - 2p | 4S + 5P |
| TABLE 4. OPT Power |
Total P layers | Primary and Secondary layer distribution. |
P&S section pattern |
| 35W to 120W | 14 p | S - 3p - S - 4p - S - 4p - S - 3p - S | 5S + 4P |
| 14p |
2p - S - 3p - S - 4p - S - 3p - S - 2p | 4S + 5P | |
| 16p |
S - 4p - S - 4p - S - 4p - S - 4p - S | 5S + 4P | |
| 16 p | 2p - S - 4p - S - 4p - S - 4p - S - 2p | 4S + 5P | |
| 18p | S - 4p - S - 5p - S - 5p - S - 4p - S |
5S + 4P | |
| 18p |
2p - S - 5p - S - 4p - S - 5p - S - 2p | 4S + 5P | |
| 20 p | S - 5p - S - 5p - S - 5p - S - 5p - S | 5S + 4P | |
| 20p |
2p - S - 5p - S - 6p - S - 5p - S -
2p |
4S + 5P | |
| 22 p | S - 5p - S - 6p - S - 6p - S - 5p - S |
5S + 4P | |
| 22p |
2p - S - 6p - S - 6p - S - 6p - S - 2p | 4S + 5P |
| TABLE 5. OPT Power |
Total P layers |
Primary and Secondary layer distribution. |
P&S section pattern |
| 120W to 500W | 10p | 2p - S - 2p - S - 2p - S - 2p - S - 2p | 4S + 5P |
| 10p | S - 2p - S - 3p - S - 3p - S - 2p - S | 5S + 4P | |
| 10p | 1p - S - 2p - S - 2p - S - 2p - S - 2p - S - 1p | 5S + 6P | |
| 10p | S - 2p - S - 2p - S - 2p - S - 2p - S - 2p - S | 6S + 5P | |
| 12p | 2p - S - 3p - S - 2p - S - 3p - S - 2p | 4S + 5P | |
| 12p | S - 3p - S - 3p - S - 3p - S - 3p - S | 5S + 4P | |
| 12p | 1p - S - 2p - S - 3p - S - 3p - S - 2p - S - 1p | 5S + 6P | |
| 12p | S - 2p - S - 3p - S - 2p - S - 3p - S - 2p - S | 6S + 5P | |
| 12p |
S - 2p - S - 2p - S - 4p - S - 2p - S - 2p - S | 6S + 5P | |
| 14p |
2p - S - 3p - S - 4p - S - 3p - S - 2p | 5S + 5P | |
| 14p | S - 3p - S - 4p - S - 4p - S - 3p - S | 5S + 4P | |
| 14p | 1p - S - 3p - S - 3p - S - 3p - S - 3p - S - 1p | 5S + 6P | |
| 14p | S - 2p - S - 3p - S - 4p - S - 3p - S - 2p - S | 6S + 5P | |
| 16p | 2p - S - 4p - S - 4p - S - 4p - S - 2p |
4S + 5P | |
| 16p | S - 4p - S - 4p - S - 4p - S - 4p - S | 5S + 4P | |
| 16p | 2p - S - 3p - S - 3p - S - 3p - S - 3p - S - 2p | 5S + 6P | |
| 16p | S - 3p - S - 3p - S - 4p - S - 3p - S - 3p
- S |
6S + 5P | |
| 18p | 2p - S - 5p - S - 4p - S - 5p - S - 2p |
4S + 5P | |
| 18p | S - 5p - S - 4p - S - 4p - S - 5p - S |
5S + 4P | |
| 18p | 2p - S - 4p - S - 3p - S - 3p - S - 4p - S - 2p | 5S + 6P | |
| 18p | S - 3p - S - 4p - S - 4p - S - 4p - S - 3p - S | 6S + 5P | |
| 20p | 3p - S - 5p - S - 4p - S - 5p - S - 3p | 4S + 5P | |
| 20p | S - 5p - S - 5p - S - 5p - S - 5p - S | 5S + 4P | |
| 20p | 2p - S - 4p - S - 4p - S - 4p - S - 4p - S - 2p | 5S + 6P | |
| 20p | S - 4p - S - 4p - S - 4p - S - 4p - S - 4p
- S |
6S + 5P | |
| 22p | 3p - S - 5p - S - 6p - S - 5p - S - 3p | 4S + 5P | |
| 22p | S - 5p - S - 6p - S - 6p - S - 5p - S | 5S + 4P | |
| 22p | 2p - S - 5p - S - 4p - S - 4p - S - 5p - S
- 2p |
5S + 6P | |
| 22p | S - 4p - S - 6p - S - 4p - S - 6p - S - 4p
- S |
6S + 5P |
| Nomex insulation |
Volts / 0.025mm rating |
Volts for thickness |
| 0.05mm |
460 |
920V |
| 0.1mm |
525 |
2,100V |
| 0.18mm |
865 |
6,228V |
| 0.25mm |
845 |
8,450V |
| 0.3mm |
870 |
10,440V |
| 0.38mm |
850 |
12,920V |
| 0.51mm |
810 |
16,524V |
| 0.61mm
|
810 |
19,764V |
| 0.76mm |
680 |
20,672V |
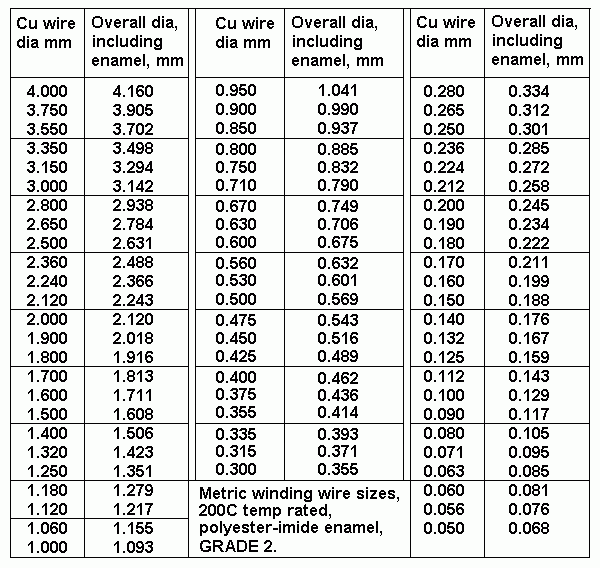
| Np = 2,320t RLa-a |
Ns = 45t, ZR 2,658 |
Ns = 48t ZR 2,336 |
Ns = 51t, ZR 2,069 |
Class A Po |
Class AB Po |
| 4k0 |
1r5 |
1r7 |
1r9 |
5W | 75W |
| 6k0 | 2r3 |
2r6 |
2r9 |
7.5W | 60W |
| 8k0 |
3r0 |
3r4 |
3r9**** |
10W | 50W |
| 12k0 |
4r5 |
5r1 |
5r8 |
15W | 35W |
| 16k0 |
6r0 |
6r8 |
7r7 |
20W | 24W |
| 24k0 |
9r0 |
10r3 |
11r6 |
18W | nil |
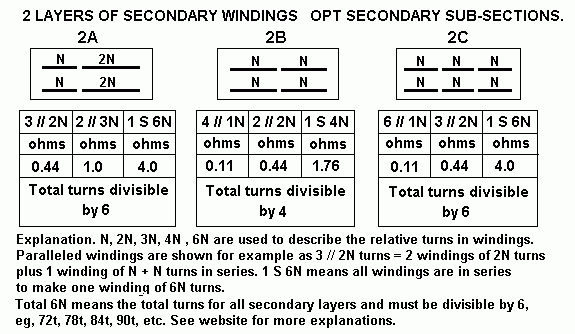
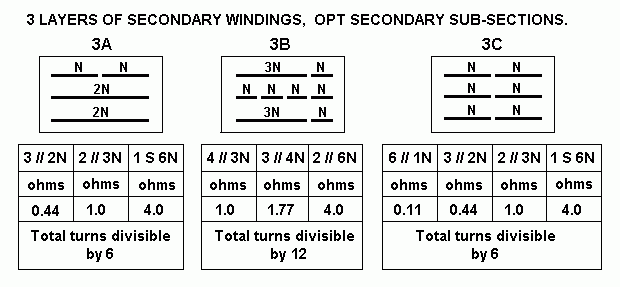
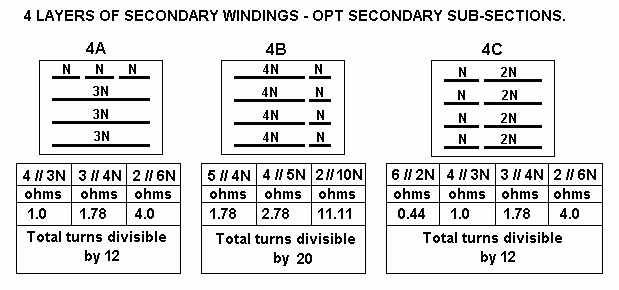
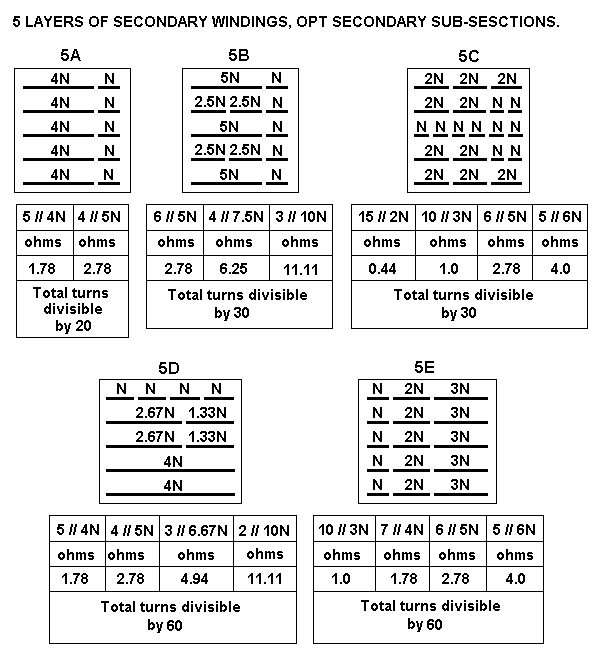
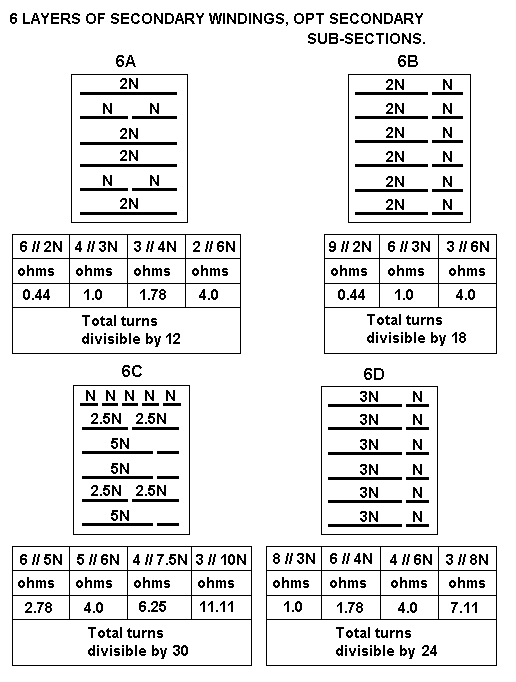
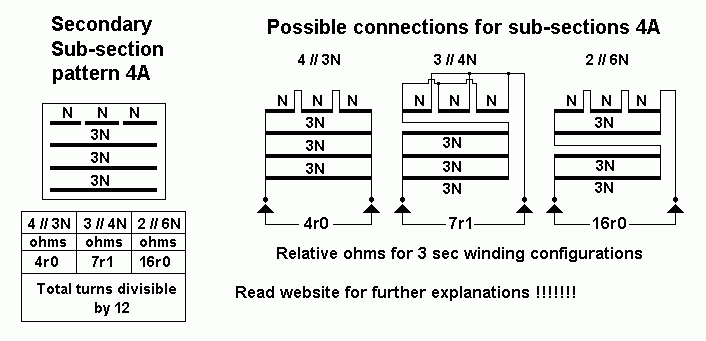
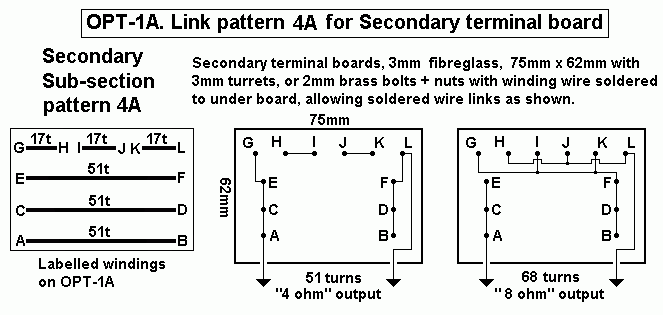
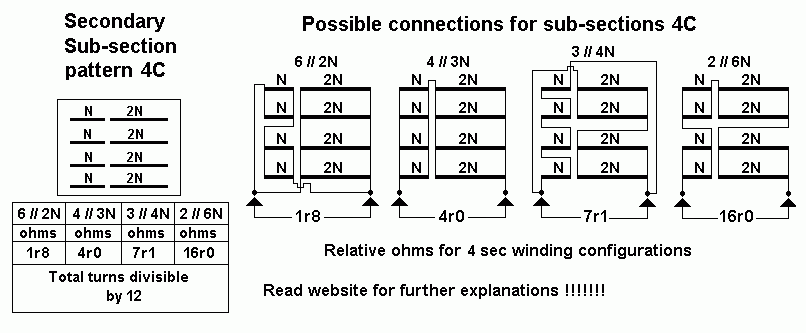
| Np = 2,320t, RLa-a |
Ns = 6 //34t ZR 4,656 |
Ns = 4 // 51t ZR 2,069 |
Ns = 3 // 68t ZR 1,164 |
Ns = 2 // 102t ZR 517 |
NS = 3 x 51t = 153t, ZR 230 |
NS = 4 x 51t = 204t, ZR 129.3 |
Class AB
power |
Class A power |
| 4k0 | 0r86 | 1r9 | 3r4** | 7r7**** | 17r4 |
30r9 |
75W | 5W |
| 6k0 | 1r3 | 2r9 | 5r1 | 11r6 | 26r0 |
46r4 |
60W | 7.5W |
| 8k0 | 1r7 | 3r9** | 6r9**** | 15r4 | 43r8 |
61r9 |
50W | 10W |
| 12k0 | 2r6 | 5r8 | 10r3 | 23r2 | 52r2 |
92r8 |
35W | 15W |
| 16k0 | 3r4** | 7r8**** | 13r7 | 30r9 | 69r6 |
123r7 |
24W | 20W |
| 24k0 | 5r1 | 11r6 | 20r6 | 46r4 | 104r3 |
185r6 |
nil | 18W |