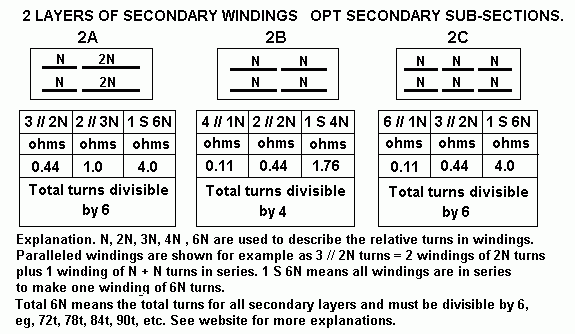
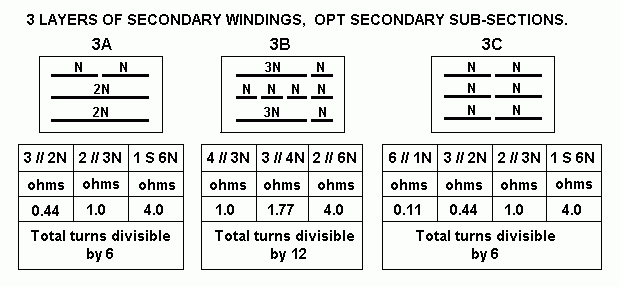
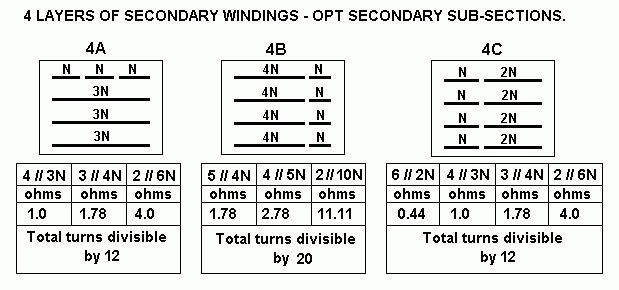
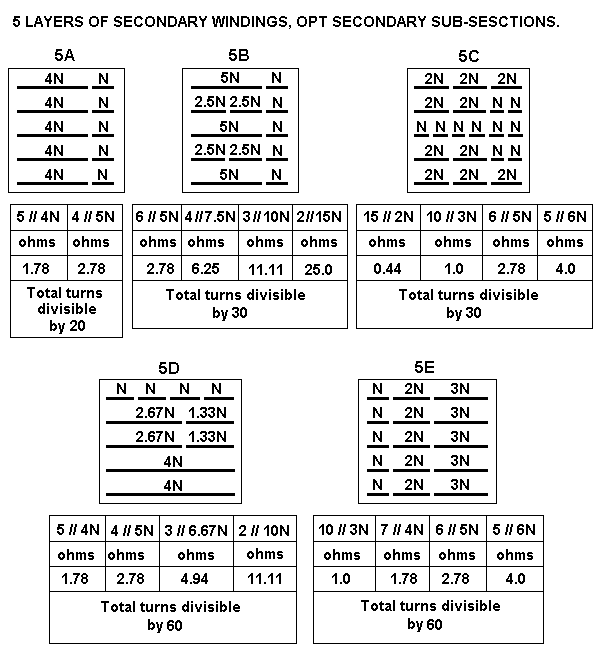
| Tube type number |
SEP,
SEBT, 50% UL, Local CFB |
Max Idle Pda W |
Ea Vdc a-k |
Ia Idc mA |
Max Po W |
Effic iency % |
Eg2 g2 to k |
Ig2 mA dc |
Pdg2 W |
RLa max Po |
| EL84 and 6V6 |
SEP, CFB, Eg2 < Ea. |
12 12 12 |
300 275 250 |
40 43 48 |
5.4 5.2 4.8 |
45 43 40 |
270 235 200 |
5 5 5 |
1.2 1.2 1.0 |
6k7 5k7 4k7 |
| EL84 and 6V6 |
SEUL, Eg2 = Ea |
12 12 12 |
300 275 250 |
40 43 48 |
5.2 4.9 4.7 |
43 41 39 |
300 275 250 |
5 6 7 |
1.2 1.4 1.5 |
6k7 5k7 4k7 |
| EL86 | SEP, CFB, Eg2 < Ea. |
12 12 12 |
250 225 200 |
48 53 60 |
5.4 5.2 4.8 |
45 43 40 |
200 200 200 |
4 5 6 |
0.8 1.0 1.2 |
4k7 3k9 3k0 |
| EL86 | SEUL, Eg2 = Ea |
12 12 12 |
250 225 200 |
48 53 60 |
5,2 4.9 4.7 |
43 41 39 |
250 225 200 |
5 6 7 |
1.3 1.4 1.4 |
4k7 3k9 3k0 |
| 807, 6L6GC, KT66, 5881 |
SEBT, CFB, Eg2 < Ea. |
21 21 21 |
400 350 300 |
53 60 70 |
9.5 9.0 8.4 |
45 43 40 |
300 270 250 |
4 5 6 |
1.2 1.4 1.5 |
6k8 5k3 3k4 |
| 807, 6L6GC, KT66, 5881 |
SEUL, Eg2 = Ea |
21 21 21 |
400 350 300 |
53 60 70 |
9.5 9.0 8.4 |
45 43 40 |
400 350 300 |
4 5 6 |
1.6 1.8 1.8 |
6k8 5k3 3k9 |
| EL34, 6CA7 |
SEP, SEBT, CFB, Eg2 < Ea |
21 21 21 |
400 350 300 |
53 60 70 |
9.6 9.5 8.4 |
46 45 41 |
270 270 270 |
7 8 9 |
1.9 2.2 2.4 |
6k8 5k3 3k4 |
| EL34, 6CA7 |
SEUL, Eg2 = Ea |
21 21 21 |
400 340 300 |
53 62 70 |
9.5 9.0 8.4 |
45 43 40 |
420 350 270 |
8 9 10 |
3.3 3.2 2.7 |
6k8 5k0 3k4 |
| Tube type number |
SEP, SEBT, 40% UL, Local CFB |
Max Idle Pda W |
Eadc +Vdc a to k |
Ia mA dc |
Max Po W |
Effic- iency % |
Eg2 g2 to k |
Ig2 mA dc |
Pdg W |
RLa max Po |
| 6550, KT88 | BT, UL, CFB, Eg2 < Ea |
28 28 28 28 |
450 390 330 270 |
62 72 85 104 |
12.6 12.0 11.5 11.0 |
45 43 41 39 |
300 270 270 270 |
5 5 6 7 |
1.5 1.4 1.6 1.9 |
6k5 5k0 3k5 2k3 |
| 6550, KT88 | UL, Eg2 = Ea |
28 28 28 28 |
450 390 330 270 |
62 76 90 110 |
12.0 11.5 10.9 10.4 |
43 41 39 37 |
450 390 330 270 |
6 7 8 10 |
2.7 2.7 2.7 2.7 |
6k5 5k0 3k5 2k3 |
| KT90, KT120 | SEBT, CFB, Eg2 > Ea |
33 33 33 33 |
450 390 330 270 |
74 85 100 123 |
14.8 14.3 12.9 12.2 |
45 43 39 37 |
300 270 270 270 |
5 6 7 8 |
1.5 1.6 1.9 2.2 |
5k5 4k2 3k0 2k0 |
| KT90, KT120 | SEUL, Eg2 = Ea |
33 33 33 33 |
450 390 330 270 |
74 85 100 123 |
14.8 13.6 13.0 12.2 |
45 43 39 37 |
450 390 330 270 |
5 6 7 8 |
2.3 2.4 2.3 2.2 |
5k5 4k2 3k0 2k0 |
| 13E1 | SEBT, CFB, Eg2 < Ea |
72 72 72 72 |
550 460 380 300 |
130 156 189 240 |
32.0 30.0 28.1 25.2 |
45 41 39 35 |
220 200 180 160 |
6 5 5 4 |
1.4 1.0 0.9 0.7 |
3k8 2k7 1k8 1k2 |
| 13E1 | SEUL, Eg2 = Ea |
70 70 70 |
375 350 325 |
186 200 215 |
27.3 25.9 22.1 |
39 37 35 |
375 350 325 |
13 12 10 |
5.0 4.2 3.3 |
1k8 1k6 1k4 |
| Tube type number |
SE triode g2 to anode. |
Max Pda +g2 idle W |
Ea +Vdc a to k |
Ia + Ig2 mAdc |
Max Po W |
Effic- iency % |
Ra at Eg1= 0Vdc |
RLa for max Po |
| EL84, |
Triode |
12 12 12 |
350 320 280 |
34 37 43 |
3.4 3.0 2.3 |
28 25 19 |
2k2 2k1 2k0 |
5k9 4k4 2k5 |
| EL86 |
Triode |
12 12 12 |
250 225 200 |
48 53 60 |
3.5 3.1 2.7 |
29 26 22 |
1k1 1k0 0k9 |
3k0 2k3 1k5 |
| 6V6 |
Triode |
12 12 12 |
370 340 317 |
32 35 38 |
3.4 3.0 1.7 |
28 25 15 |
2k5 2k4 2k3 |
6k5 4k9 3k7 |
| 807, 6L6, KT66, 5881 |
Triode | 22 22 22 22 |
500 450 400 350 |
44 49 55 63 |
7.3 6.7 5.5 4.2 |
33 30 25 19 |
1k9 1k8 1k8 1k7 |
7k8 5k6 3k7 2k2 |
| 6CM5, EL36 | Triode | 18 18 18 |
375 350 325 |
48 51 55 |
7.6 7.5 7.4 |
42 41 40 |
0k6 0k5 0k5 |
6k6 5k8 4k9 |
| EL34, 6CA7 | Triode | 23 23 23 23 |
450 420 390 360 |
51 55 59 64 |
7.5 7.3 6.9 6.6 |
33 32 30 29 |
1k2 1k1 1k1 1k0 |
7k4 4k8 4k0 3k3 |
| 6550, KT88 | Triode | 30 30 30 30 |
500 450 400 350 |
60 67 75 86 |
11.0 11.0 10.0 8.4 |
36 36 30 28 |
1k0 0k9 0k9 0k9 |
6k3 4k9 3k5 2k3 |
| KT90 | Triode | 33 33 33 33 |
500 450 400 350 |
66 73 83 94 |
13.4 12.6 11.8 10.3 |
39 38 35 31 |
0k7 0k7 0k7 0k7 |
6k2 4k8 3k5 2k4 |
| KT120 | Triode | 40 40 40 40 |
500 450 400 350 |
80 88 100 114 |
15.6 14.7 13.5 11.0 |
39 36 33 27 |
0k7 0k7 0k7 0k7 |
4k9 3k8 2k7 1k7 |
| 45 |
Real Triode |
8 8 8 |
270 240 210 |
29 33 38 |
2.4 2.0 1.4 |
30 25 17 |
1k8 1k8 1k8 |
5k7 3k7 1k9 |
| 2A3 | Real Triode |
12 12 12 |
300 275 250 |
40 43 48 |
4.4 4.2 3.9 |
36 35 32 |
0k9 0k9 0k9 |
5k7 4k6 3k4 |
| 300B | Real Triode |
28 28 28 |
420 380 340 |
66 74 82 |
10.8 10.0 9.3 |
37 35 33 |
0k7 0k7 0k7 |
5k0 3k8 2k8 |
| 845 | Real Triode |
75 75 75 |
1,100 950 800 |
68 78 93 |
27.1 23.7 18.2 |
36 31 24 |
2k2 2k2 2k2 |
11k8 7k8 4k2 |
| GM70 |
Real Triode |
75 75 75 |
1,100 950 800 |
68 78 93 |
29.1 26.1 22.0 |
38 34 29 |
1k8 1k8 1k8 |
12k6 8k6 5k1 |
| 13E1 |
Triode | 70 70 70 |
375 350 325 |
186 200 215 |
24.0 23.0 22.0 |
34 32 31 |
0k3 0k3 0k3 |
1k4 1k2 1k0 |
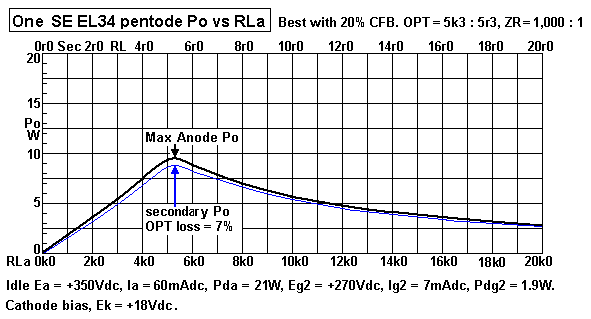
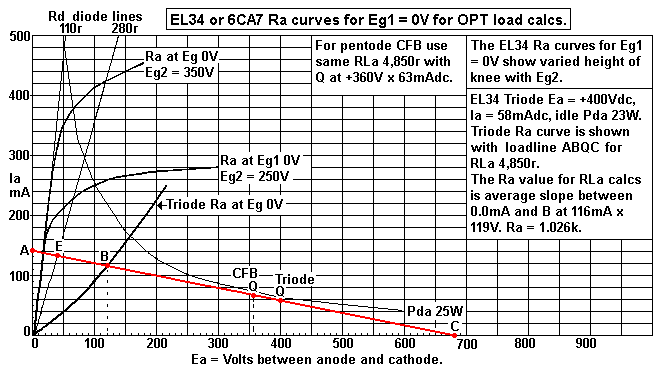
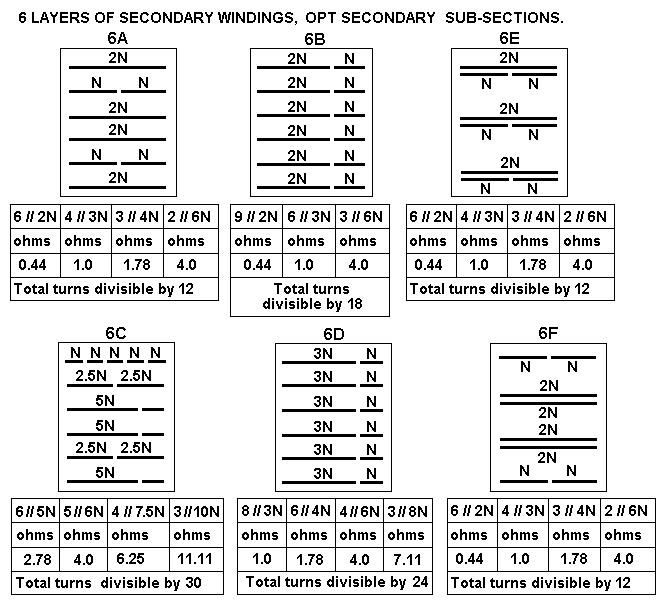
| Secondary Po |
50W to 100W |
32W to 50W |
10W to 32W |
5W to 10W |
| Afe constant | 450 |
483 |
516 |
550 |
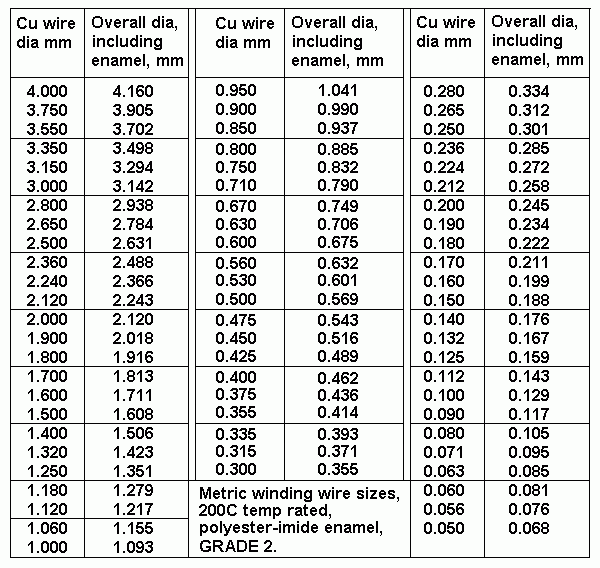
| 7W
to 15W |
10 to 20 | 2p~4p - S - 4p~8p - S - 4p~8p - S - 2p~4p | 3S
+ 4P |
| 7W to 15W |
10 to 20 |
S - 4p~6p - S -
4p~6p - S - 4p~6p - S |
4S + 3P |
| 0W to 15W |
Total P layers |
Primary and Secondary layer
distribution. |
P+S section pattern |
| 0 to 7W |
10p to 24p |
S - 10p~24p - S |
2S + 1P |
| 7W to 15W | 10p to 20p | S - 5p~10p - S - 5p~10p - S | 3S + 2P |
| 7W to 15W |
10 to 20 | 2p~4p - S - 4p~8p - S - 4p~8p - S - 2p~4p | 3S + 4P |
| 7W to 15W |
10 to 20 |
S - 4p~6p - S
- 4p~6p - S - 4p~6p - S |
4S + 3P |
| 15W to 30W |
Total P layers |
Primary and Secondary layer distribution. | P+S section pattern |
| 12p | 2p - S - 4p - S - 4p - S - 2p | 3S + 4P | |
| 12p | S - 4p - S - 4p - S - 4p - S | 4S + 3P | |
| 13p |
2p - S - 3p - S - 3p - S - 3p - S - 2p | 4S + 5P |
|
| 14p | 2p - S - 3p - S - 4p - S - 3p - S - 2p | 3S + 4P | |
| 14p | S - 5p - S - 4p - S - 5p - S | 4S + 3P | |
| 15p |
S - 5p - S - 5p - S - 5p - S | 4S + 3P |
|
| 16p | 3p - S - 5p - S - 5p - S - 3p | 3S + 4P | |
| 16p | S - 4p - S - 4p - S - 4p - S - 4p - S | 5S + 4P | |
| 16p | 2p - S - 4p - S - 4p - S - 4p - S - 2p | 4S + 5P | |
| 18p | 3p - S - 6p - S - 6p - S - 3p | 3S + 4P | |
| 18p | S - 4p - S - 5p - S - 5p - S - 4p - S | 5S + 4P | |
| 20p | 3p - S - 7p - S - 7p - S - 3p | 4S + 3P | |
| 20p | S - 7p - S - 6p - S - 7p - S | 5S + 4P | |
| 20p | 2p - S - 5p - S - 6p - S - 5p - S - 2p | 4S + 5P | |
| 22p |
2p - S - 6p -
S - 6p - S - 6p - S - 2p |
4S + 5P |
|
| 22p |
S - 7p - S -
8p - S - 7p - S |
4S + 3P |
| 30W to 100W |
Total P layers |
Primary and Secondary layer distribution. | P+S section pattern |
| 13p |
2p - S - 3p - S - 3p - S - 3p - S - 2p | 4S + 5P |
|
| |
14 p | S - 3p - S - 4p - S - 4p - S - 3p - S | 5S + 4P |
| 14p |
2p - S - 3p - S - 4p - S - 3p - S - 2p | 4S + 5P | |
| 15p |
S - 5p - S - 5p - S - 5p - S | 4S + 3P |
|
| 15p |
2p - S - 4p - S - 3p - S - 4p - S - 2p | 4S + 5P |
|
| 16p |
S - 4p - S - 4p - S - 4p - S - 4p - S | 5S + 4P | |
| 16p | 2p - S - 4p - S - 4p - S - 4p - S - 2p | 4S + 5P | |
| 18p | S - 4p - S - 5p - S - 5p - S - 4p - S |
5S + 4P | |
| 18p |
2p - S - 5p - S - 4p - S - 5p - S - 2p | 4S + 5P | |
| 19p |
2p - S - 5p - S - 5p - S - 5p - S - 2p | 4S + 5P |
|
| 20 p | S - 5p - S - 5p - S - 5p - S - 5p - S | 5S + 4P | |
| 20p |
2p - S - 5p - S - 6p - S - 5p - S -
2p |
4S + 5P | |
| 21p |
3p - S - 5p - S - 5p - S - 5p - S - 3p | 4S + 5P |
|
| 22 p | S - 5p - S - 6p - S - 6p - S - 5p - S |
5S + 4P | |
| 22p |
2p - S - 6p - S - 6p - S - 6p - S - 2p | 4S + 5P |
| 100W to 250W |
Total P layers |
Primary and Secondary layer distribution. | P+S section pattern |
| |
10p | 2p - S - 2p - S - 2p - S - 2p - S - 2p | 4S + 5P |
| 10p | S - 2p - S - 3p - S - 3p - S - 2p - S | 5S + 4P | |
| 10p | 1p - S - 2p - S - 2p - S - 2p - S - 2p - S - 1p | 5S + 6P | |
| 10p | S - 2p - S - 2p - S - 2p - S - 2p - S - 2p - S | 6S + 5P | |
| 12p | 2p - S - 3p - S - 2p - S - 3p - S - 2p | 4S + 5P | |
| 12p | S - 3p - S - 3p - S - 3p - S - 3p - S | 5S + 4P | |
| 12p | 1p - S - 2p - S - 3p - S - 3p - S - 2p - S - 1p | 5S + 6P | |
| 12p | S - 2p - S - 3p - S - 2p - S - 3p - S - 2p - S | 6S + 5P | |
| 12p |
S - 2p - S - 2p - S - 4p - S - 2p - S - 2p - S | 6S + 5P | |
| 13p |
2p - S - 3p - S - 3p - S - 3p - S - 2p | 4S + 5P |
|
| 13p |
S - 3p - S - 4p - S - 3p - S - 3p - S | 5S + 4P |
|
| 13p |
S - 2p - S - 3p - S - 3p - S - 3p - S - 2p - S | 6S + 5P |
|
| 14p |
2p - S - 3p - S - 4p - S - 3p - S - 2p | 5S + 5P | |
| 14p | S - 3p - S - 4p - S - 4p - S - 3p - S | 5S + 4P | |
| 14p | 1p - S - 3p - S - 3p - S - 3p - S - 3p - S - 1p | 5S + 6P | |
| 14p | S - 2p - S - 3p - S - 4p - S - 3p - S - 2p - S | 6S + 5P | |
| 16p | 2p - S - 4p - S - 4p - S - 4p - S - 2p |
4S + 5P | |
| 16p | S - 4p - S - 4p - S - 4p - S - 4p - S | 5S + 4P | |
| 16p | 2p - S - 3p - S - 3p - S - 3p - S - 3p - S - 2p | 5S + 6P | |
| 16p | S - 3p - S - 3p - S - 4p - S - 3p - S - 3p
- S |
6S + 5P | |
| 18p | 2p - S - 5p - S - 4p - S - 5p - S - 2p |
4S + 5P | |
| 18p | S - 5p - S - 4p - S - 4p - S - 5p - S |
5S + 4P | |
| 18p | 2p - S - 4p - S - 3p - S - 3p - S - 4p - S - 2p | 5S + 6P | |
| 18p | S - 3p - S - 4p - S - 4p - S - 4p - S - 3p - S | 6S + 5P | |
| 19p |
S - 3p - S - 4p - S - 5p - S - 4p - S - 3p - S | 6S + 5P |
|
| 20p | 3p - S - 5p - S - 4p - S - 5p - S - 3p | 4S + 5P | |
| 20p | S - 5p - S - 5p - S - 5p - S - 5p - S | 5S + 4P | |
| 20p | 2p - S - 4p - S - 4p - S - 4p - S - 4p - S - 2p | 5S + 6P | |
| 20p | S - 4p - S - 4p - S - 4p - S - 4p - S - 4p
- S |
6S + 5P | |
| 21p |
S - 4p - S - 4p - S - 5p - S - 4p - S - 4p - S | 6S + 5P |
|
| 21p |
3p - S - 5p - S - 4p - S - 5p - S - 3p | 4S + 5P |
|
| 22p | 3p - S - 5p - S - 6p - S - 5p - S - 3p | 4S + 5P | |
| 22p | S - 5p - S - 6p - S - 6p - S - 5p - S | 5S + 4P | |
| 22p | 2p - S - 5p - S - 4p - S - 4p - S - 5p - S
- 2p |
5S + 6P | |
| 22p | S - 4p - S - 6p - S - 4p - S - 6p - S - 4p
- S |
6S + 5P |