CHOKES - PAGE 1.
Updated 2017.
This page 1 is about :-
A. What is a choke? General information about inductance and
filter chokes.
B. Simplest choke measurement.
Fig 1. Schematic for measuring choke without Idc.
C. MEASURE CHOKE EXAMPLE :-
Steps 1 to 10.
D. Iron cored inductance and permeability µ and µe.
E. Testing chokes for CLC with Idc.
Fig 2. Schematic for testing choke with Idc.
Steps 1 to 7.
F. LF resonance of CLC filters.
Fig. F response of low pass LC filter.
G. Alternative CRCRC to CLC
H. Bypassing choke with R+C for damped 100Hz resonance.
I. Hanna's method of choke design, RDH4.
J. Design a choke for 270mAdc and up about 6H.
Table 1, wire sizes for Grade 2 winding wire.
Table 2, choke details based on T25mm x S25mm E&I.
Steps 1 to 9.
K. Winding chokes.
----------------------------------------------------------------------------------------------------------
For chokes in PSU with CLC filters with high Idc, low Vac across
L, you are at Chokes 1
For chokes in PSU with LC filters with high Idc and high Vac
across L, go to Chokes
2
For chokes for high or low Idc feed to anode with high AF across
L, go to Chokes 3
(A) What is a "Choke"?
I do not know why anyone named a coil of wire to be a "choke", but
very soon after
electricity was put to use in many ways by 1900, people were
winding coils of insulated
copper wire around iron to make an inductance to inhibit the flow
of ac, alternating
current, Iac, or to "choke the flow" of ac, alternating current.
At early time in our knowledge of electronics, inductance was
found to have 1,001
uses in coils and transformers for power transmission, telegraph
and phone
communications and radio transmitting and reception. Inductance is
a good filter
element to reduce unwanted Iac flow between point A and B in a
circuit. The right
quantity of inductance with low wire resistance and low shunt
capacitance makes a
very simple rugged filter element. But the choice for a choke
depends on the application,
size, weight, cost and perhaps and several other factors.
The mathematics I have here is most basic and is free of quantum
physics which
surround behavior of inductors. There is enough necessary maths to
enable most people
wanting to make a good choke in a workshop. Definitions of
Inductance do exist
elsewhere on the Internet, and most people could be completely
bamboozled by
mathematics.
Basically, if there is change of current through a coil of
enamelled wire there will be a
change of magnetic field produced. The field has direction just as
the north - south
direction of Earth's magnetic field "poles". But with a coil
subject to applied Vac and with
Iac, the field direction changes with direction of current. The
applied energy is described
as Magnetic Motive Force, MMF, expressed as the current x turns,
or At. The MMF, is
often stated simply as F, but not confused with F for frequency,
so context is king, OK.
The F causes production of a magnetic field. For Idc, the field is
constant, and does not
cause any opposition to Idc flow in wire.
Where there is Vac applied across a coil, there is Iac and a
changing magnetic field
which changes direction and magnitude.
This change of Vac produces an "electro motive force", EMF, which
opposes the
change in the flow of the Iac.
This phenomenon is difficult to understand.
Where there is only Idc in the coil, there is a fixed magnetic
field ( like Earth's ).
Consider a typical iron cored filter choke coil with 2,000turns
and wire resistance = 50r.
With +5Vdc across coil, there is 0.1Adc. This coil acts like a 50r
resistance where t
here is only 0.1Adc flow. If the Vdc is instantly switched to
-5Vdc, there is no instant
change of current, but I change will occur slowly, until current =
0.1Adc in the opposite
direction. The magnetic properties of the coil are opposing the
current change when
rapid change occurs. If a 5Vrms x 100Hz sine wave is applied
across this coil, the Ia
change may be found to be only 2.3mArms. The coil behaves like a
resistance with
R = 5V / 0.0023A = 2,174r. If the sine wave is at 50Hz, the Iac =
0.0046MArms,
and the apparent resistance has changed to 1,087r. Thus the choke
resistance varies
with to frequency of applied V. The coil inductance, L, has the
property of a reactance,
XL, for which the unit is the ohm, or r.
XL = 2 x pye x Frequency x L, where pye is a constant for all
equations = 22 / 7 = 3.14286,
Frequency is in Hertz, Hz, ie, wave cycles per second,
and L is Henry, the unit of inductance named after Joseph Henry,
an American scientist
who died in 1879.
With Iac and Iac, any conductor creates a magnetic field around
itself. The field around a
piece of wire is fairly weak, but where many turns are wound into
a coil, the magnetic field
lines around each wire combine together to become much stronger,
and a magnetic field
has a direction along centre line of coil then spreading out at
one end of coil and returning
to the other end.
An invisible magnetic loop is formed. It can be most clearly seen
where an electro magnet
is sprinkled with iron filings. There is no pattern to the filings
with no Idc. But Idc is switched
on, the filings immediately form lines which show where the lines
of magnetic field exist.
When Vac is applied across a coil, there is Iac flow and the field
changes with frequency
and it opposes the flow of Iac where the frequency is high enough.
If iron filings are sprinkled
on a coil with say 50Hz current, they are less likely to show the
pattern of lines because the
direction of field changes 50 times a second and the filings jump
about a fair bit, and do not
illustrate what is really going on. With 5Vrms x 100Hz applied
across the coil with 2,000t,
the field strength is much less than there was with 5Vc across the
coil.
It is the Change of applied Voltage which changes the magnetic
field which creates
opposition to the current flow. The opposition to current flow
when Vac is applied to a coil.
If the frequency was 0.001Hz, barely above 0.0Hz, there is not
much opposition to current flow.
But at 100Hz, there may be a lot of opposition, and much less Iac
flows, and at 10kHz,
almost no Iac flow. A piece of wire 25mm long has a very small
amount of inductance.
But the reactance XL at 1GHz may be so high it is difficult to get
Iac to flow. So all modern
circuitry operating at such high F must have extremely short
connecting wires and small
circuits within ICs, and any understanding of what exactly happens
in an IC can become
a mystery. Magnetism is at work, among other things.
Electro-magnets are used in many industrial applications. In early
loudspeakers before
permanent magnets were able to be made, the anode Idc supply
current was fed through a
field coil to generate a strong magnetic field in an annular gap
between a rod of iron and a
surrounding plate. The cylindrical voice coil worked with the dc
magnetic field across the gap
to produce motion to create sound waves.The speaker was a kind of
electric motor.
The speaker electro magnet was known as a "field coil" and had
thousands of turns of fine
wire carrying say 50mAdc to a 6V6 in an old AM radio. The 50mAdc
in say 5,000turns gave
F = 0.05A x 5,000t = 250At, and the iron of the speaker is
arranged to make an electro
magnet with iron path length of about say 200mm, but including a
gap of say 2mm in which
the magnetic field intensity may be a fixed 1.2Tesla in one
direction.
In this annular gap, the voice coil attached cone can move with
the high Iac and low Vac
producing a force to make cone move.
This old fashioned method of building an early electromagnetic
speaker was invented in
1930s, and the coil to produce the intense magnetic field for
voice coil was called a
"field coil" and was used to filter the B+ produced by HT winding
and diodes and caps
to allow hum-free sound from the radio.
During early 1930s, the same basic idea of using many turns of
wire on a core of iron was
used in chokes to filter out Vac content while allowing easy flow
of Idc. Many old radios
had a field coil which had L = maybe 5H, and filter caps for CLC
were typically 8uF or 16uF,
and expensive, and unreliable. A modern electrolytic with same
size as 1935 16uF x 450V
rated may now have 470uF x 450V, and is much cheaper, and more
reliable.
Many tubed amplifiers still use CLC filtering for their B+ anode
supplies to reduce the
Vac at B+ rails to extremely low levels to allow tube operation
from a supply that is like a
large 400Vdc battery, but of course the 400Vdc cannot be
maintained when mains power
is turned off.
The term "impedance" is also used for a choke but usually it
should be called reactance
because wire resistance and winding self capacitance have
negligible effect on operation
and calculations for the intended use at 50Hz or 100Hz in PSU, or
where frequencies are
between 14Hz and 50kHz for choke feed for Idc to anodes. Impedance
is the name used
for networks of two or more L, C or R elements with at least one
being L or C, and with all
being relevant to the operation.
A filter choke in PSU have L reactance XL, plus wire resistance
Rw. The Rw is often ignored
in some calculations for Vac but is relevant for Idc calculations
where the Vdc across Rw is
important to design the Vdc supply for the whole circuit to work.
The LCR model of a coil is
the pure L + Re in series, with its shunt C across the L+R.
A choke for CLC may have 3.4H and have Rw = 50r. At 14Hz, XL =
6.28 x 14 x 3.4 = 298r.
The impedance includes Rw 50r and.
ZL = sq.rt ( XL squared + Rw squared ) = sq.rt ( 89,358 +
2,500 ) = 303r. So the 50r has
very little contribution to the reactance XL. For series R+L, Rw
makes very little difference
to the total Z where XL > 10 x Rw.
For all series L + R,
impedance Z ( L+R ) = Square root of ( Rw squared + XL squared )
ohms, r.
For all parallel L // R,
impedance Z ( L // R ) = 1 / sq.rt ( 1 / R squared + 1 / ZL
squared ) ohms, r.
Most electronics behavior is governed by fairly simple
mathematics, so remember this
phenomenon, and remember to leave a lot of your silly common-sense
behind when you
enter the world of electronics, or you will be lost.
Unfortunately, the simple electronics can turn into a huge
nightmare of complexity when
more than 3 LCR elements are connected. I found that all the free
software to enable
calculation of passive LCR networks vanished from the Internet to
be replaced by programs
you must pay for. There are a few CAD programs for free which I
found always far too
difficult to use because the NERDS who wrote the codes have zero
ability to teach
anyone else anything. The Help offered by many apps and programs
turns out to be
Dead Useless.
Where possible, Rw should be minimized to avoid unwanted Vdc drop
across choke Rw
and to avoid heat dissipation.
(B) Simplest choke measurement without Idc :-
Fig 1.
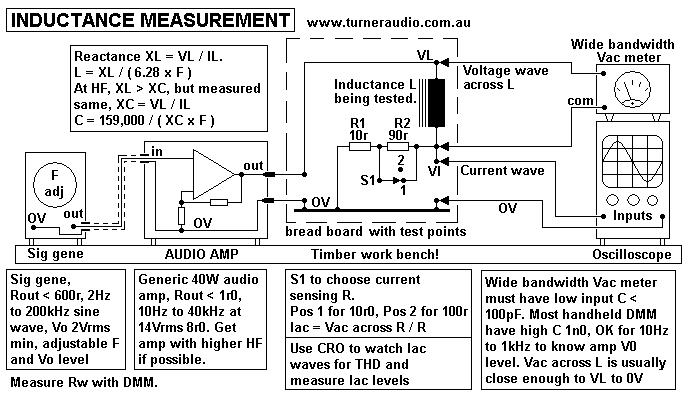
Fig 1 shows an inductance being measured. Similar set up can also
be used for
measuring capacitance values. The test circuit may be set up on
panel of plywood
say 200mm square, with 12mm x 4 gauge brass cupboard screws for
connection
points and bare 1mm dia Cu wire used for links. Rotary wafer
switches can be
mounted on a number of screw heads or on a metal panel near one
edge of board.
Tools needed :-
A good signal generator, able to make 2Hz to 200kHz, sine wave,
square wave, with
accurate F indication. Possible frequency meter if signal gene has
a dial with poor
calibration. Oscilloscope ( CRO ) with bandwidth up to at least
1MHz. Many are 15MHz,
dual trace, but single trace is OK.
40W audio amp, bandwidth 7Hz to 50kHz, -3dB points, to give 15Vrms
at least, Rout < 1r0.
Vac meter with multi ranges and bandwidth of 5Hz to 200kHz and
giving Vrms.
Most DMM are useless for anything below 10Hz and above 2kHz and
have Cin = 1nF
which loads the choke so once you have measured the Vac at 1kHz to
be say 10Vrms at
VL, you know what amp Vac will be for say 10Hz to 30kHz. Do not
clip Vac meter across
choke.
The measurements are all made by applying Vac across choke from
low Z Vac source,
and measuring Iac flow in either 10r0 or 100r.
The Vac across 10r0 or 100r will mostly be much lower than Vac
from amp.
RCA leads, voltmeter leads and amplifier leads.
Solder, patience, persistence, and the will to understand and to
never assume anything.
Note book and pencil.
Computer, i-pad, mobile phone and keyboard are NOT NEEDED, or damn
well
wanted anywhere near any man trying to understand basic
electronics without feeling
bored, or that he should be doing something else, which afflicts
over 50% of everyone.
R1 is simple toggle switch, use a rugged one. It allows choice of
current sensing R
of 10r or 100r and if the choke has short circuit or is low L air
core type, the amp has
lowest possible load of 10r0 so amp should never be damaged, and I
know of course
that where something can be Pharqued Arpe, it will be, if idiots
are present.
Some zealous folks would want dual trace CRO and set it up to view
VL to 0V on chan A
and Vac across R1+2 on chan B.
This is a super good idea, you NEED to know if any THD appears
which may render
measurements to be bullshit.
The CRO allows anyone to see the distortion in an iron cored choke
at VI.
THD from sig gene and amp should be < 0.5% and usually hard to
see on CRO, but you
will see 5% easily if the choke begins to saturate with LF Vac.
If air cored inductances are measured, they should not produce any
THD,
The signal generator should give the same constant Vo for say 2Hz
to 200kHz but
F and level is adjustable. Sig gen Rout should be < 600r so
that connection to a small
power amp input does not have any effect on sig gene Vo level.
Many "Signal generators"
or "Function generators" have "decade" ranges say 2Hz to 20Hz,
20Hz to 200Hz and so
on up to 200kHz which an audio tech uses to test audio gear. The
better and more
expensive but fragile function generators have a top frequency of
2MHz, with dc
offset, sine wave, square wave, triangular wave, maybe saw tooth
wave, FM and
AM modulation etc. But for this test you only need sine waves.
This test schematic does not include ability to measure with Idc
flow in choke.
Those of you who insist on Idc being present, make a variable
constant current
source between +40Vdc rail so that its impedance and capacitance
ads no parasitic
R or C that spoils the measurement of L measured. The Idc may
cause choke to
saturate but that is OK, you will measure that, but the CCS will
remain invisible.
The amp used can be any generic solid state audio amp capable of
40W to 8r0
= 17.88Vrms max, but most audio power amps have F range of say 5Hz
to 30kHz
at max Po and maybe slightly more F at 1/2 Po for 12.6Vrms.
Testing with amp
level set for 10.0Vrms at 1kHz is good start.
L values could be between 0.1mH and 500H.
(C) MEASURE CHOKE EXAMPLE :-
Wasteless pattern E+I choke, T25mm x S25mm, Core material quality
is unknown.
Its age indicates if could have been made in 1960 with NOSS
E+I.
Turns are unknown, I are are butted to E with small unknown air
gap.
Random winding pattern without layers and insulation.
Magnetic length and average turn length for this core size =
138mm.
(1) The wire size looks to be approximately 0.42mm oa dia using
micrometer, so Cu
dia = 0.35mm Cu dia. Iron ML = 139mm, average turn length TL =
139mm.
Rw measures = 47r.
Now Rw = N turns x ML mm ( 44,000 x Cu dia squared ).
Thus N turns = Rw x ( 44,000 x Cu dia squared ) / TLmm
= 47r x ( 44,000 x 0.35mm x 0.35mm ) / 138mm = 1,835t.
Check if this is possible. For T25mm material, bobbin winding area
available for wire
= 33mm x 10mm = 330sq.mm.
If oa dia wire = 0.42mm, then max N can be 330sq.mm / 0.42mm
squared = 1,872.
For random winding, the turns are always less than theoretical so
N could be 1,835t,
depending on exact size of wire. Assume N =1,800t.
(2) Set S1 for R1 = 10r0. Unknown choke is connected to VL and VI
points.
(3) Set signal gene to give 10.0Vrms at VL to 0V at 1kHz from
audio amp. Measure VI across
10r0 and you may 0.0062Vrms, tiny, and maybe not correct, so
switch for 100r,
Then you might measure 0.062Vrms and Iac = 0.062 / 100r =
0.62mArms.
XL = 10.0V / 0.62mA = 16.1k.
L = XL / ( 6.28 x F ) = 16,100r / ( 6.28 x 1,000Hz ) =
2.57H. Use of higher or lower Vac may give
slightly different L result.
(4) Repeat the measurements with same VA, but at 500Hz, 200Hz,
100Hz, 50Hz, and 25Hz
if possible. THD may begin to exceed 10% at LF.
The choke is to be used for CLC filter if possible. Therefore its
properties at 100Hz are important.
Measurement at 100Hz with VL = 10.0Vac could give 0.318Vac at
100r, so Iac = 3.18mArms.
XL = 10V / 0.00318 = 3,140r.
L = XL / ( 6.28 x F ) = 3,140r / ( 6.28 x 100Hz ) = 5.0H.
Don't be surprise to find L at 1kHz is a bit less at 100Hz. This
is because even with an air gap,
the L value varies because the iron µ value varies with F, and so
does µe, but the the L varies
much more without an air gap than with an air gap.
(5) What is the ue for the choke?
"µe" is the effective core permeability for the F and Vac
amplitude used for the test.
Calculate µe at 100Hz.
Inductance for coil with E+I core or C-core =
L = 1.26 x N squared x Afe x µe / ( 1,000,000,000 x iron ML )
1.26 and 1,000,000,000 are constants for metric measurements, L in
Henry, N = turns,
Afe = Tmm x Smm of core, ML in mm.
Therefore µe = L x 1,000,000,000 x ML / ( 1.26 x N squared x
Afe )
= 5.0H x 1,000,000,000 x 139mm / ( 1.26 x 1,800t x 1,800t x 25mm x
25mm ) = 272.
Now this µe is much less than the max possible µ with all E+I
maximally intermeshed
which could be between 1,500 for worst old iron and 10,000 for
real good GOSS.
Adding Idc through the winding magnetises the core but because
there is an air gap the
Bdc change from no Idc to a lot of Idc may not change the µe or
measured XL very much.
As air gap increases µe reduces and so does L. Idc makes less
difference to L provided
the core is not saturated by Idc and the applied Vac does not
cause core to saturate.
It is planned to use the choke with Bdc up to maybe
0.8Tesla.
For this choke, if Idc = 150mAdc for 2 output tubes,
Bdc = 12.6 x N x Idc x µe / ( 10,000 x ML ) where Bdc is
Tesla, 12.6 and 10,000 are
constants, N is turns, Idc in Amps dc, µe is calculated number
that is thought to be true,
ML is iron magnetic length in mm.
Bdc = 12.6 x 1,800t x 0.15A x 272 / ( 10,000 x 139 ) = 0.67Tesla.
This tells you that you could have more Idc, but core is not
saturated.
Core might saturate at 1.1Tesla. The Bac possible = 1.1T - 0.67T
= 0.43Tesla.
Now N = Vrms x 226,000 / ( Afe x Bac x F )
so Vrms max = max Bac x Afe x N x F / 226,000
For this choke, max Vrms at 100Hz = 0.43T x 625sq.mm x 1,800t x
100Hz / ( 226,000 )
= 214Vrms.
At this Vac, the choke should begin to saturate, but the test gear
cannot supply
214Vrms to find Fsat, from which we might more accurately know the
max possible Bac.
Because there is no Idc, max Bac might be 1.1T to max Vac could be
547Vrms.
If the F was reduced to 10Hz, the Vac for 1.1T would be 54.7Vac,
no Idc.
With Idc, Vac max may be 21.3Vrms.
It becomes difficult to work out exact properties any more than I
show here but you can
tell if the choke is usable, or if it has a fault like a shorted
turn.
If the above choke is used in CLC filter with C1 = 47uF where Vac
at C1
= 10.3Vrms x 100Hz, and if C2 = 220uF, and if L = 5H, the XL at
100Hz = 3,140r.
XC2 220uF at 100Hz = 159,000 / ( 220uF x 100Hz ) = 7.2r.
Vr ripple voltage at 100Hz at C2 can be calculated = Vac at C1 x
XC2 / XL at 100Hz
= 10.3Vrms x 7.2r / 3,140r = 0.024Vrms.
This indicates quite good attenuation factor = Vo / Vin = 0.024V /
10.3V
= 0.00233, ie, 1 / 429, or - 52dB attenuation.
The full properties of this choke may be found where it is working
in a PSU.
The air gap might be adjusted down a little to increase µe for L =
7H and that
would increase attenuation factor to 1 / 600. The resonant Fo for
7H and 220uF
= 5,035 / sq.rt ( L mH x CuF ) where Fo is frequency Hz, and 5,035
is a constant.
Fo = 5,035 / ( 7,000mH x 220uF ) = 4.0Hz which is nicely lower
than the AF band
official beginning at 20Hz.
(6) All chokes have some capacitance between layers of windings
which sum to
form the "self capacitance" of the winding when measured from one
end of the
winding to the other. There is a small amount of C between
adjacent turns of wire
which adds up to be significant. For PSU choke in above test, self
C < 300pF.
It forms a parallel resonant circuit with the L. To find Fo with
above test circuit will
be difficult because the Q of the LC resonance is low, maybe 1.0,
and the L
value may have halved at somewhere above 1kHz, and unless you know
what
L is as F rises then the Fo for self resonance is impossible to
calculate.
But you should measure XL rises with increasing F above say 30Hz
where it
may be lowest at 1.32k to 32k at 1kHz and 60k at 5kHz and then the
ZL
curve levels and reduces above 20kHz. The reduction of XL is due
to the
shunt C of choke plus oscilloscope probe C which could be
100pF.
If a graph is drawn for XL from say 10Hz to 40kHz, you may see a
curve like the
Sydney Harbour Bridge.
The XL for 5H at 10Hz = 314r, 3,140r for 100Hz, maybe 16k at 1kHz,
and somewhere
above 1kHz the XL will begin to reduce at a rate of -6dB per
octave and that is effect
of shunt C between winding ends. The XL continues to rise, but the
XC becomes a
falling value as F is increased. The L and C form a parallel
resonant L+C circuit where
the maximum XL occurs at the top of the bridge curve. The
attenuation rate of -6dB
per octave is at F above the maximum XL.
If shunt C = 200pF, then at 40kHz, XC = 19.8k, and 10V across this
gives 0.5mA
so you would see 0.05Vac across 100r, and at 80kHz if you could
have 80kHz
it would be 0.1Vac where XC = 10k.
Theoretical Fo for resonance for Cshunt and L cannot be predicted
because L reduces
as F rises while C remains fixed. But if the choke is to be used
to feed Idc to an anode
to give a high impedance load of at least 2k0 for most AF then the
choke should be OK.
Fo for all LC =5,035 / sq.rt ( L x C ), where Fo is in Hz,
5,035 is constant for all equations,
L = milli-Henry mH, C = uF.
(7). But whatever Csh exists, it is able to pass some of the diode
HF switching noise pulses
which are a bunch of HF oscillations above 50kHz occurring 100Hz
rate. These often
manage to get into audio path and are clearly seen on CRO at amp
output with amplitude
up to 10mVpk. It makes a harsh noise if its amplified. But the
choke is often not the real cause.
The noise may get into audio path via 0V path because the HF
switching pulses can travel
easily in low impedance 0V rail. The connections of diodes and HT
secs must be done so
Vac from HT winding is applied to reservoir C without including
any length of 0V rail.
Star earthing also helps.
I found using 0.47uF x 630V polyester; across C1 and C2 electros
of CLC helped and
0.05uF 1,000V across HT windings. Keep 0V paths correctly short,
and keep input circuits
and NFB wires away from PSU. DO NOT use the chassis as the 0V
rail.
When ALL noise of any kind at amp Vo = 0.25mV with input shorted
to 0V with RCA
shorting plug, you have a low noise power amp. If an amp makes
28Vrms max for 100W to
8r0, SNR is considered = 100dB, good, by any standard, but where
Vo = 1Vrms, SNR
= 72dB, also excellent. I have measured and fixed dozens of noisy
amps.
(8) For choke measured above, it may be impossible to use it for a
choke input supply
for where you have HT winding with diodes feeding choke then a
reservoir C.
If B+ was say +400V, the HT Vac for LC input will be near to Vdc /
0.88. So for +400V,
you need Vac = 400 / 0.88 = 454Vac. The amplitude of 100Hz applied
to choke =
about 0.45 x HT Vac = 0.45 x 454Vrms = 204Vrms.
Now if you want 150mAdc for LC input, then the L must be RLdc /
900 Henry for where
Idc = minimum, or in this case 15mAdc, 1/10 of the working Idc, So
you must have a
bleeder R for 15mAdc = 27k rated for 10W. The L must be 27,000r /
900 = 30H, and the
5H above would be useless because it is only 5H.
Chokes 2
explains it further.
(9) What is max Idc for 5H choke above? Rw = 47r with 0.35mm Cu
dia wire.
Acu = 0.096sq.mm.
If max current density = 3A / sq.mm, max Idc = 3 x 0.096 = 288mA.
This makes heat = Idc squared x R = 0.288 squared x 47r = 3.9W.
BUT, the winding
would get hot, and the 288mAdc is far more than wanted and would
cause core saturation
but would not fuse the winding within a minute.
If Idc = 150mAdc, then heat is 1W and core is happy. Current
density = 1.56A / sq.mm = OK
With 150mAdc, Vdc across choke = 7.05Vdc = small % of B+ = OK.
(10) Air cored inductors have advantages for many AF and RF
applications but it is difficult
to make large useful amounts of inductance without using iron
cores. An air cored 10H filter
choke without iron core and with Rw = 50r may be 50 times larger
than the iron core
choke and would be an expensive waste of copper.
For crossover filter chokes for speakers, attenuator networks in
amplifiers, etc, air cored
chokes are often used because the amount of inductance required is
usually less than 50mH
and they create no distortion, are fairly cheap to make, have
constant L value for all levels
of Vac, and work from DC to RF, and there is never any saturation.
Some crossover coils used in series with bass speakers obstruct HF
signals have
pre-moulded iron dust cores or a bar made of stacked laminations
in a solenoid design
to increase L and keep winding R low. Usually the bar cored
solenoid choke raises L by
a factor of only 4 above that for the same coil with no iron core.
Inductance is roughly proportional to number of turns squared,
although for air cored L,
Wheeler's formula works well to calculate air core inductance. The
size and shape of the
coil matters with air cored L. But if there is a centre hole big
enough for a bar of lams using
some spare Is from a transformer, the L may increase by about 4
times. Using GOSS bar
keeps THD low, but rules for Bac apply.
It is always best to only use air cored L in series with bass
speakers to exclude HF.
The Rw should always be less than 1/10 of the speaker impedance in
its centre of
bandwidth, so if a 4r0 speaker has Z = 3r0, then a 2.4mH choke
should have Rw > 0.3r,
for cut off = 200Hz.
Hi-end crossover coils are very large to minimize Rw losses. And
very expensive.
But the size becomes lower as F rises for midrange drivers and
tweeters so there is
no need for any iron in L for speaker crossovers.
Good speaker design follows all the rules about LCR theory.
Some of the larger air core crossover coils can have a bar core
added to make a 4mH
choke into 16mH, which has XL = 10r0 at 100Hz, so they may be used
for CLC in a
PSU.
So for CLC with 2 x 4,700uF plus 16mH, 100Hz attenuation factor =
0.035. This could be
for 2Adc for input tube heaters, or for a solid state PSU and Vr
at C2 = 32mVac.
However, the 2Adc produces Bdc in bar, but ue is very low at say 4
because the air gap
is longer than iron ML, so the Bdc may not be very high.
For filter chokes in power supplies, we really only need to know
what the inductance
will be at 100Hz, because rectifier ripple frequency = 2 x mains
50Hz UK, Europe,
Australia, and elsewhere. Any power supplies built in "50Hz"
countries will work fine
where 60Hz mains exists in the USA. Some iron wound components
such as power
transformers designed for 60Hz operation in USA may not work well
when exported to
50Hz countries. I am Australian, and all my formulas in this site
are based around 50Hz
mains and I use metric measurements unless stated otherwise.
The above test circuit may have its R values varied further as
desired if your reasoning
is correct. Practice with measuring and calculating should train
you to work precisely
without guessing or assuming one single thing. The dedicated
technician avoids making
amplifiers riddled with noise or with a bad smoking habit.
The pure L or the C reactance has NO resistance and therefore
current flow does not
dissipate any heat, and no work is done in the L or C. But where
the Iac or Idc lows in
wire resistance in leads, heat is produced and heat Power = R x
Irms squared, or
Power = Vac squared / R, in Watts.
Energy is transferred by the L or C and can be temporarily stored
but not lost if the
L or C is perfect, ie, has low resistance wire or leads, and no
power is lost on heating
and iron core due to hysteresis phenomena.
.
The energy in a choke becomes stored in its magnetization.
Increasing Iac in choke
increases Vac across choke, and increases the magnetic field and
energy store. Reducing
Iac in choke causes opposite V change direction across choke as
magnetic stored energy is
released. Please search Google for more extensive explanations
about inductance and
capacitance properties because most people remain ignorant of such
basic ideas and
thus cannot ever learn to properly design their amplifiers. Once a
"hands on"
understanding of how L, C and R behave with AC signals, then other
concepts become clear.
---------------------------------------------------------------------------------------------------------------------------
(D) The iron cored inductance.
The L value changes for applied Vac levels and frequency. For a
pure sine wave Vac
applied across an iron cored inductor there are distortion
currents generated in the iron
due to what is called hysteresis. Nobody seems to be able to
explain EXACTLY what
hysteresis is, in terms normal ppl understand. Most blokes know
what a hysterical shiela
is alright, a woman who is crying, laughing and machine gunning
your ears with bullshit.
BUT, those who want know what hysteresis does need only examine
the magnetic
properties of any mains transformer winding on a core with no air
gap.
The current wave is ALWAYS 90 degrees behind the applied Vac
across the coil and
the distortion in current waves is low with a small Vac for lo Bac
of less than say 0.3Tesla.
But as Bac increases above 0.3T, the distortion becomes visible on
a CRO and if Bac
= 1.4T, the distortion currents may have risen above the level of
fundamental frequency,
so the the impedance of the coil reduces and core heats up because
some of the input
V x I power is converted into heat. The core heating is due to
"eddy currents", and to
reduces these to a minimum the lamination thickness must be
reduced so GOSS
material is often never thicker than 0.35mm. See my Graph 3 and 4
at
powertranschokes.html.
So what we need to know about an iron cored L is its suitability
for a position in a circuit
as PSU filter L in CLC network. High Z anode dc supply for a
triode, etc.
Usually, maximum inductance is wanted without any core saturation
of a choke or
transformer.
Chokes in tube amps are rarely ever without Idc flow. Most have
Idc flow in one direction
only in one winding, but a few have Idc flow in opposite
directions away from a CT in one
winding. Thus the working effective permeability, µe, is usually
less than the maximum
possible µ for any given magnetic core material, and one or more
"air gaps" are inserted
into the magnetic path length of the iron core.
The reduced µe gives less Idc caused magnetization, Bdc, while not
saturating the iron,
and allowing additional magnetisation by Iac, Bac, and the sum of
Bdc and Bac should
never exceed the maximum B quoted in data for the material.
Most iron-wound inductors found in chokes and OPT in tube audio
amps use Grain
Oriented Silicon Steel, GOSS, aka Cold Rolled Silicon Steel, CRGO.
Toroid coils wound on GOSS cores have the highest µ up to 40,000.
They are useless for where any Idc flow is used, in chokes, SE or
PP OPT.
But it is splendid material for a PT, providing the windings have
woven insulation to
allow easy varnishing and the transformer is potted. Few are, so I
never bought many.
It is difficult to add an air gap to a toroid to reduce its µ to
say 4,000 for a PP OPT
or to 400 for a choke.
C-cores are exceptionally good for chokes and all OPT. Air gapping
is very easy.
and maximum µ could be 15,000, and it is easily reduced to any
smaller value by placing
non magnetic material into the two gaps between the two C that
make up a C-core O shape.
GOSS C-cores with their two cuts polished are excellent for PT and
give low losses and the
ZL curve shows that distortion currents are low at the onset of
core saturation which is often
at 1.2T. Toroids and C-cores have the lowest eddy currents at
mains frequencies so have
lowest loss of Watts / Kg. C-cores
made by Nicore.com are also excellent. But I have no idea
where small quantities may be purchased.
GOSS sheet can be cut into E and I shapes to make E+I cores. It is
often 0.35mm thick.
The GOSS material favoured by ppl making tube gear is known as M6,
and AK Steel in USA
The raw material for transformer cores comes in rolls of material,
maybe 1M wide x 0.35mm
thick and the grain direction is along the length of the roll.
The E are stamped from the roll in pairs of E facing each other
and two I come from the
material between the three E legs.
Thus grain direction is along each of 3 legs of E and along the I.
But when assembled to
make E+I core, the magnetic "lines of force" run along each E leg
easily but then flows at
degrees to get into E upright with difficulty, and if you consider
the assembled E+I core,
the path length includes material with lower µ because of grain
direction so the max µ for
E+I is usually never as high as for C-cores or a toroid.
And it seems this inherent character of E+I show that the ZL
curves I have plotted for
GOSS show distortion currents increasing above about 0.5T, and the
wound coil and core
has much steeply reducing ZL above 0.5T. But there is no need to
worry about this until
Bac gets to 1.2T or maybe 1.5T, depending on the use and nature of
E+I.
The E+I is thus OK for a PT or OPT if Bac = 1.2T if the load value
for the winding is well
below the non loaded XL value at 1.2T.
Where the applied Vac produces Bac above 0.5Tesla the E+I core
begins to saturate,
and up to 1.2T the pure inductance seems non linear but the core
still works well enough
to be a high enough impedance if the load value is typically many
times lower than XL
at 1.2T. Above 1.2T, the distortion currents in core become high
enough to make the
Z ( RL // XL ) generate significant distortion in Vac across the
RL // XL, and where this
is say 5% THD at say 1.2T, there cannot be any higher Vac applied.
For any Bac increase above say 1.2T, the peak Iac becomes rapidly
higher and if Vac
is say doubled, the core would behave as a magnetic inductance up
to 1.2T, but for 2.4T
the coil acts as a piece of wire, ie, the coil winding resistance.
I had customers who had bought CD players online from USA meant
for 115Vac mains input.
They eagerly unpacked the item here in Australia and plugged it
into our 240Vac mains and
within 1/2 a second the item was totally wrecked, because Vdc
rails went to twice normal
value and then the mains transformer winding fused and then the
mains fuse blew.
They were made more unhappy when I advised them the item was not
fixable.
So it is important to know the properties of the iron being used
for any project you have.
The iron values are both queer and vague, and the God Of Triodes
did try to work out a
better deal with the God Of Steel, who is a terribly stubborn
entity. You need to know
anything with turns around iron is a puzzle, but if you can deal
with variable parameters
you will understand. So tell yourself, in a loud voice "Understand
This Coil ! " and if you do
not, coils around iron will always be a Miss Terry.
------------------------------------------------------------------------------------------------------------------------------
(E) Testing chokes for CLC filters with Idc,
setting the air gap.
I have sometimes had to supply filter chokes or SE OPTs to people
building tube amps and have
set the air gap prior to the sale but without the real amp circuit
present.
Fig 2. Test schematic for measuring choke L with Idc, and
setting air gap.
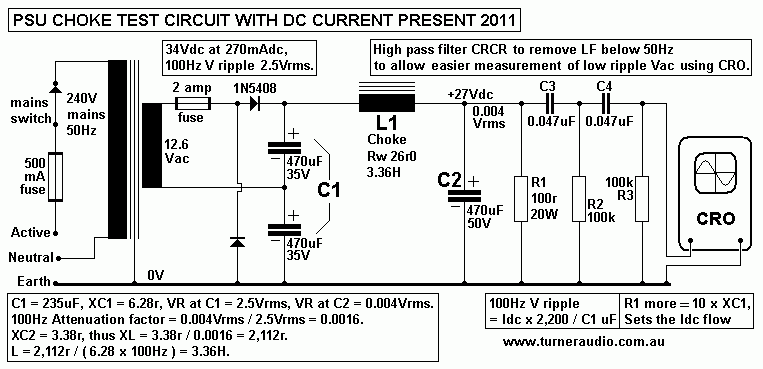
The Fig 2 circuit will allow safe measurement of a filter choke
using a cheap 30VA PT
12.6Vac secondary for up to 2.4Aac. 2 x 1N5408 Si diodes are used
with 2 x 470uF
caps in a doubler rectifier to make up to 34Vdc at 0.8Adc.
Providing the Idc and C values
are the same as in an amplifier with a much higher B+, the 100Hz
Vac ripple calculations
and filtering action of the CLC will be exactly the same. The Idc
is 270mAdc for the anode
supply for 4 x EL34 plus driver stage.
(1) Any surplus transformer with winding over 12.6Vrms to 30Vrms
may be used in either
bridge, full wave, or doubler config to give Vdc at C1 not higher
than +40Vdc, but be aware
of the VA rating. The choke has Rw 26r, R1 is adjusted so Idc =
270mAdc in this case.
(2) The air gap must be adjusted to maximize the inductance to get
high Vac attenuation
but not have the choke become saturated.
Fig 2 shows the Vr before and after L, and with L1 air gap
adjusted for optimum.
100Hz attenuation factor = Vripple after choke / Vripple before
choke = 4mVrms / 2.5Vrms
= 0.0016, or 1 / 625.
XC2 470uF = 3.38r at 100Hz. XLP = 625 x XC2 = 625 x 3.38r = 2,112r
Thus L = 2,112r / ( 6.28 x 100Hz ) = 3.36H.
The Rw of 26r has almost no influence on design, but the the Idc
flow heats the wire and
heat power = Rw x Idc squared = 26 x 0.27A x 0.27A = 1.9W,
and the temperature rise
may be calculated according to table for power / sq.ins. A choke
less with slightly less surface
area than a tennis ball should withstand 1.9W.
(3) The choke may first be set up with Is tightly butted against
Es, and even without any
air gap the butted join acts like there has been an air gap added.
So for a core rated for max µ between 10,000 to 2,500 with maximum
intermeshing may have
hard butted µe = 2,000 to 700 approx, without any real air gap.
Butting a pile of E against I pile
means the grain direction of Is and Es changes direction by 90
degrees, and this much reduces
µ by making the effective ML behave as though it is longer than it
really is, and this is similar
to adding a small air gap, even though no real air gap exists.
Therefore placing a real air gap should follow the formulas for µe
and air gap. Butted µ should be
considered to be say 1,000 in calculations.
Where µ = 1,000, it is high enough for many core with Idc to
become saturated, ie, Bdc is between
1.0Tesla for low grade iron to 1.6Tfor good GOSS E+I.
(4) The 100Hz Vr at C1 = Idc x 2,200 / C in uF, Vrms. 2,200 is
constant for 100Hz ripple.
For Vr 120Hz, use 1,833 instead of 2,200.
For Fig 2, Vr at C1 = 2.5Vrms.
If the core is saturated, the Vr at C2 will be higher than
expected as the Iac flows from C1 to C2 via
the Rw 26r without much attenuation by inductance. The CLC becomes
CRC, and Vr at C2 could
be 0.32Vrms.
Adding a small air gap with a sheet of paper ( say 0.07mm ) right
across the space between E and I
may reduce Bdc to below saturation, and allow the choke to work as
a pure inductance.
This total gap = 0.14mm, because there are 2 gaps around the
magnetic length which is the centre
line in steel around each window.
The Vac at C2 should reduce, but if not much, add another sheet of
paper for 0.14mm, and air gap
= 0.28mm, and you get less Vac at C2. You can keep adding sheets
of paper until Vac at C2 is very
low and then if any more sheets of paper are added, the Vac at C2
begins to rise. This means the
air gap is too large, the choke L has begun to reduce because µe
has become too small.
So use the number of sheets of paper that give Vac minimum at C2.
(5) The air gap is correct when the wanted Idc is flowing, and the
Vr at C2 is at its minimum.
The measurement of Vac across C2 is almost impossible to do with a
DMM or analog meter
because the +Vdc rail will contain a lot of noise below 30Hz
because the mains level is constantly
changing due to the hundreds of other ppl sharing your 240V mains
supply.
Its expensive to regulate the +Vdc rail, and the simple option is
to use a RCRC filter with -3dB
pole at 50Hz, say 0.33uF + 10k0 and two cascaded filters give -3dB
at 70Hz with only -1dB at 100Hz
but - 40dB at 7Hz and more below that and then the CRO trace used
to see the Vac at C2
will not bounce up and down so much you cannot see what you want
to measure. The CRO screen
should have a piece of tape alongside giving between 0 and 1mV
with range setting for smallest
Vac range.
There is no way of knowing exactly what the Bdc may be for a choke
with Idc because µe cannot
be exactly known, but it can be calculated if N, Vac, Afe and F is
known.
Measuring L of choke without Idc is not best practice because the
addition of Idc will reduce
slightly the µe without Idc and best measurement is done
with Idc flow equal to what is found
in the amp where choke is to be used.
The wave at C1 will be a sawtooth or triangular wave which
contains many even numbered
H products, ie, 200Hz, 400Hz. The Vac at C2 will have mainly
only 100Hz.
(6) The paper thickness must be known. A 128 page exercise
book has 64 sheets and has
4.7mm total thickness not including cardboard
covers. Each paper sheet thickness = 4.7mm / 64 = 0.073mm. It is
important to measure the gap.
Paper is OK for a permanent gap if well soaked with varnish before
bolts and yokes are drawn up
tight. Re-measuring after tightening bolts should give the same
results.
Soaking the choke in a can of varnish before bolts are tight is
best way to wet all surfaces.
When bolts are tightened, excess varnish can flow back to can. The
choke may be heated
slightly to dry and harden varnish.
(7) The 470uF or more between OPT B+ connection to 0V contains a
huge reserve of energy,
like a battery, and transients in music in class AB amps pull the
extra instant Iadc from this
capacitance, say C2. In all the cases of 30W AB amps, rarely does
the B+ move more than +/- 1V
even with very loud music passages. If Idc falls below the rated
Idc, Inductance slightly increases,
and filtering is improved. The choke value swings a little in
response to the Idc demands.
---------------------------------------------------------------------------------------------------------------------
(F) Resonance in CLC filters.
Fig 3.
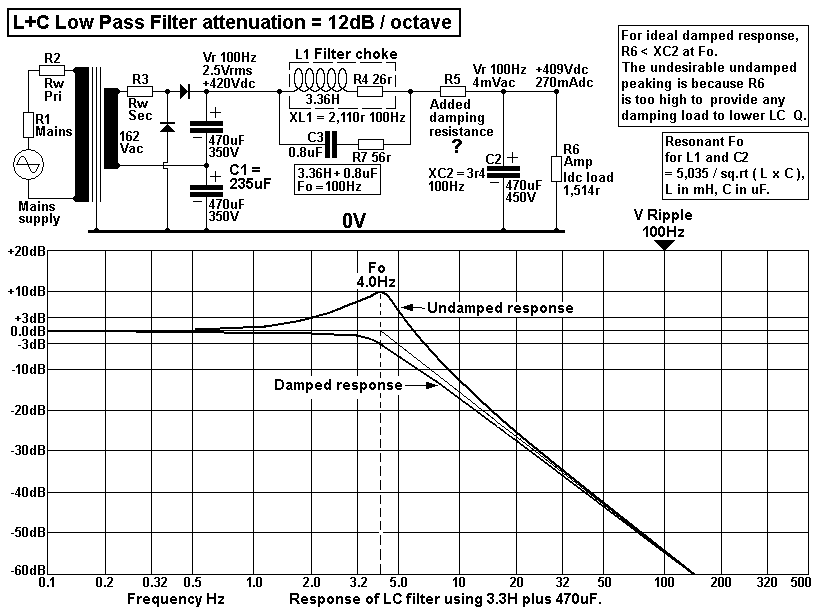
Fig 3 shows the same 470uF caps and 3.36H choke in CLC for a tube
amp.
Wherever there is a CLC ripple filter as in Fig 3 above, there
will be series resonant behavior
between L1 and C2.
The resonant F = Fo = 5,035 / sq.rt ( LmH x CuF ).
If the L = 3,360mH, and C2 = 470uF, then Fo = 4.0Hz. At 4.0Hz, XL
= XC = 84r.
The 100Hz Vr at C1 is generated by diodes and HT winding on PT. I
show R1 source
resistance for Mains, which may vary, but is usually < 5r0 for
240Vac Mains.
The PT has R2 Rw = about 2.5% of the primary load. R3 secondary Rw
may be 2.5%
of the sec load estimated at 200r. The Si diodes have R < 1r0,
so may be ignored.
But total source resistance of Vdc supply including C1 may total
about 5% x Vdc / Idc = 5%
of 1,555r = 78r. It is much higher if there are tube diodes and HT
winding Rw is deliberately
high to make sure the Rw limits the peak charging current in tube
diodes to their rating
which is many times less than max peak Iac in Si diodes.
The F response graph is typical for CLC filter in a B+ PSU. For
the flattest F response for
L1+C2 below say 10Hz. R6 should be = 1.414 x XL
at 4Hz = 118r.
But R6 shown is the load of the tubes shown here = 1,514r, and
this is not low enough to
reduce Q of L1 and C2.
To damp the resonance, R could be in series with L1 and C2, so R5
could be added to
ensure the flat response.
Flattening the F response means that the noise between 2Hz and 8Hz
created by
mains Vac level changes can be reduced by -10dB.
The L1 Rw of 26r does some damping, but 26r is too low to do all
damping, so R5 may be
118r - 26r = 92r, where Vac source resistance
= 0.0r. When I plotted the response above, the test circuit may
have had very low source R.
If source R = 78r, then peaking
will be low, maybe less than +2dB, and R5 omitted. In theory, R5 =
118r - 78r - 26r = 14r,
so may be omitted.
If the choke is allowed to have high Rw, it just gets too hot.
It is surely easy to build an amp where CLC has a peaked LF
response with Fo resonance
between 3Hz and 15Hz where the 10Hz at C2 connection at OPT is
higher than at C1.
If C2 = 3 parallel 470uF = 1,410uF, Fo = 2.3Hz, and the XC2 = 49r.
The R for non peaked
response = 68r, and if Rw = 26r, and
source R = 78r, there should be no peak in LF response. But this
does not means there
will be no LF below 15Hz at C2. There is always some.
Typical LF at C2 below 15Hz = 0.03Vac, and well above the 100Hz
level of 0.004Vac.
Noise with F below 10Hz usually cannot easily reach the listening
ear because speakers
cannot reproduce it, and we cannot hear it, and if the amp is a PP
type, the OPT common
mode rejection action prevents such LF noise getting to OPT
Sec.The effect on amp operation
of B+ wobbling up and down +/- 50mVpk is entirely negligible. The
mains should be able to
be switched on and off at 1 second intervals and no change in
sound should occur.
I have never seen a need for B+ regulation, not even with SE amps
which have no benefit
of common mode rejection of rail noise
with a PP OPT with CT.
--------------------------------------------------------------------------------------------------------------------------------
(G) The alternative to CLC is CRCRC with more C and maybe more
R.
For worthwhile 100Hz attenuation factor = 0.1, a section of R+C
should have R > 10 x XC.
If the B+ = +420Vdc at C1 235uF, and we allow B+ reduction of 5%
with filter,
the Vdc output after filter = +420Vdc - 5% = +399Vdc. The Vdc
across filter R =
( 420Vdc - 399Vdc ) / 0.27A = 77r, and it must have 15W
rating.
If CRCRC is used, each R = 38.5r, say 3 x 100r x 5W ea in parallel
for R = 33r.
If C = 470u, 100Hz Xc = 3.4r so attenuation = 0.1 approx, so at
C3, expect Vripple =
2.5Vrms x 0.1 x 0.1 = 0.025Vrms.
If C2 and C3 = 940uF each then Vripple at C3 = 2.5Vrms x 0.05 x
0.05 = 0.0063Vrms
which I suggest is quite low enough for any amp, and there will be
no problem with
LF resonance.
I could argue that the choke is good, but the extra 3 x 470uF plus
6 x 100r are going
to be cheaper, and not use up too much space on chassis. There
will be no resonant LF
behavior for the CRCRC.
One problem with a total of 6 x 470uF in B+ supply is the inrush
Ia needed to charge
them all up after amp turns on. Series Rw at PT primary may be
40r, so where heater
filaments are cold, and 6 x 470uF have no Vdc, peak input current
could be high enough
for long enough time to blow a 4A slow-blow fuse which can
withstand 4A average with
higher peaks.
My common solution to reducing high inrush Iac to at least 1/2 the
value was to have
about 80r in series with primary of PT, and then have a relay
which shunts the 80r after
about 4 seconds. So B+ reaches about +280Vdc in about 3 seconds
with a 2A slow fuse,
and when 80r is shunted, B+ continues to +420Vdc, and the second
surge of high input
Iac is no more than the first, so the 2A fuse does not blow.
Normal mains power input for
say 4 x KT88 in 5050 may be 200W, so Iac = 0.83Aac, so the fuse
should blow when
something causes Iac input to increase to say 2.4A. The 4A fuse
may allow something
to heat up and catch fire before a fuse blows.
A delayed B+ on every tube amp is not a bad idea, even where CLC
with less C is used.
The delay should work where amp is switched off, then on again
within 2 seconds.
The LC filter is a simple good filtering solution but the LF
resonance should be kept
below 5Hz. The amp should have C+R input network to attenuate
input below 5Hz.
With a preamp, the Idc is much less, and tube load is usually much
higher ohms than
in a power amp so a choke is never needed. Plain CRCRC filters
work very well without
wasting much power in hot resistors. A shunt regulator at preamp
input stages usually
keeps the VLF from appearing at output, especially where there is
a MC phono amp
which has very high LF gain, and where there is a possibility of
LF oscillations.
(H) Any choke in a CLC supply may be bypassed with suitable R+C
in series to
make a damped parallel resonant L+C 100Hz.
See Fig 3, R7 = 56r, more than Rw, and C3 = 0.8uF. C is polyester
630V rated, and
calculated when the choke inductance is known, then adjusted in
circuit for least V2 at C2.
For L = 3.36H, C will be about 0.8uF. This will reduce 100Hz at C
by -10dB, but some
200Hz and 400Hz manage to pass, but will remain below 2mVrms at
C2.
-------------------------------------------------------------------------------------------------------------------
(I) One very good method to design a filter choke for CLC
use is to work from
first principles with Hanna's method clearly spelled out in the
Radiotron Designer's
Handbook, 4th Ed, 1955, pages 247 to 250. But I have never found
time to convert
Hanna's Method to metric units which were introduced to Australia
in the 1960s, so
anyone using Hanna's Method will have to work with inch
dimensions.
There is another good little book, 'Coil Design and Construction
Manual' B.B. Babani,
first printed 1960, except that it does not delve into air gap
setting very well.
When I use Hanna or Babani to check my design for a choke, I must
go back to using
Imperial measures of inches which I still know well, but its a
Royal PIA for ppl who
never used inches and feet, and know only Metres, M, and
millimetres, mm.
(J) Design a choke for 270mAdc, and with L up to 6H.
Not all of you will beg borrow or steal a copy of RDH4, and most
men never read books
any more.
I offer an alternative and include a typical example most everyone
will find useful at
some time if they build any tube amp supply which needs a supply
from 50mAdc to
270mAdc, and for any B+ voltage from +250Vdc to +550Vdc. It is not
to dissipate
more than 4W in Rw.
(1) Calculate wire size.
Current density for design should be 2Adc / sq.mm. This usually
allows a fault condition
where Idc could double for a awhile without heat damage to wire
and insulation.
For 2A / sq.mm, Cu section area = Idc / 2A / sq.mm.
So for 270mA, Cu area = 0.27A / 2 = 0.135sq.mm and Cu dia wire =
sq.rt ( Cu area x 28 / 22 )
= sq.rt ( 0.135 x 28 / 22 ) = 0.414mm.
You could try 0.40mm Cu dia x 0.462mm oa dia, see wire table 1 :-
Table 1. Wire sizes for Grade 2 winding wire.
Table 2. Choke details based on based on T25mm x S25mm
wasteless E+I, with
area in bobbin for wire = 34.0mm x 10.0mm = 340sq.mm.
Cu wire
dia, mm |
turns,
max. |
Resistance,
ohms |
DC current
max |
L, Henry
µe =200 |
0.20
|
4,800
|
380
|
89mA
|
25.0
|
0.25
|
3,100
|
157
|
138mA
|
10.8
|
0.30
|
2,200
|
77
|
197mA
|
5.4
|
0.35
|
1,600
|
42
|
267mA
|
2.88
|
0.40
|
1,300
|
26
|
339mA
|
1.9
|
0.45
|
1,050
|
17
|
420mA
|
1.24
|
0.50
|
870
|
11
|
522mA
|
0.85
|
0.60
|
600
|
5.3
|
752mA
|
0.40
|
0.75
|
390
|
2.2
|
1.16A
|
0.17
|
1.00
|
230
|
0.73
|
2.02A
|
0.06
|
1.40
|
120
|
0.19
|
4.0A
|
0.016
|
2.00
|
60
|
0.05
|
7.7A
|
0.004
|
Note. Above I said 0.40mm Cu dia x 0.462mm oa dia could be used
and window
winding area = 340sq.mm.
The table suggests turns = 1,300t for 0.4mmCu wire.
Neat layer winding and 0.05mm insulation will allow tpl = 0.97 x
34mm / 0.462mm = 71t.
The winding height of 10mm allows no of layers = 10.0 / ( 0.462mm
+ 0.05mm )
= 19.53 layers, but you should 20.0 layers so total turns = 71tpl
x 20L = 1,420t.
Random winding will allow about 1,300t.
(2) Calculate Rw.
Rw = TL x N / ( 44,000 x Cu dia squared ).
For T25mm x S25mm, TL = 138mm. Rw = 138mm x 1,420 / ( 44,000 x
0.4mm x 0.4mm )
= 28r.
Heat in winding = Rw x Idc squared = 28r x 0.27A x 0.27A = 2.04W.
On page 238, RDH4, there is Fig 5.18B giving Temp rise versus
W / square inch of
external core area.
Graph 1. Power transformer temperature rise, degrees C
for Watts heat loss per sq.inch.
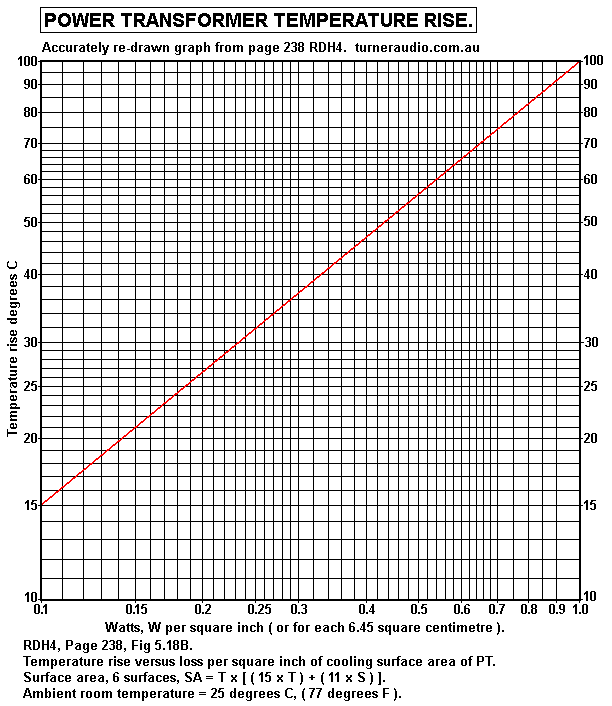
SA = T x [ ( 15 x T ) + ( 11 x S ) ].
For T25mm x S25mm wasteless E+I, T = S = 1 inch.
SA = 1 x [ ( 15 x 1 ) + (11 x 1 ) ] = 26 sq.ins.
Heat per sq.in = 2.04W / 26 = 0.078W / sq.in and T rise = less
than 15C.
There is no heating of core from high Bac, so choke runs
cool.
(3) What are other core T size options?
Try T32mm x S32mm for Afe = 1,024sq.mm. Winding area = 43mm x
12.8mm = 550sq.mm.
For 0.462 oa dia wire, expect get 90tpl x 25L = 2,250t, maybe
2,000t with random l winding.
TL = 180mm. Rw = 2,250 x 180mm / ( 44,000 x 0.4mm x 0.4mm ) = 58r.
For 270mAdc, Heat = 4.22W. SA = 40sq.in. W / sq.in = 4.22 / 40 =
0.1055W / sq.in.
Temp rise = 15C. running temp = 40C = OK.
(4) To avoid complete reliance on Table 2 above, Calculate
µe for T25mm x S25mm.
Bdc = 12.6 x N x Idc x µe / ( 10,000 x ML ) where Bdc is
Tesla, 12.6 and 10,000 are
constants for all such equations, Idc is Amps dc, µe is effective
core permeability
with air gap, ML is iron magnetic path length around each window
in mm.
For 1,420t, Bdc for GOSS core can be 1.0Tesla = 12.6 x 1,420t x
0.27A x µe / ( 10,000 x 138mm ).
Thus µe = 1.0T x 10,000 x 138mm / ( 12.6 x 1,420t x 0.27A ) = 286.
(5) Calculate L for µe = 286, T25mmx S25mm.
L = 1.26 x Nsquared x Afe x µe / ( 1,000 x ML ) where L is
Henry, 1.26 is a constant,
N is thousands of turns, Afe is centre led area = Tmm x Smm, µe is
effective permeability
with air gap, ML is iron magnetic path length around each window.
For this choke, L = 1.26 x 1.42th squared x 25mm x 25mm x 286 / (
1,000 x 138mm ) = 3.3H.
(6) Calculate L for T25mm x S50mm.
For same 1,420t, µe, 0.27Adc, ML,
L = 1.26 x 1.42 squared x 25mm x 50mm x 286 / ( 1,000 x 138mm ) =
6.6H.
(7) Calculate ue for T32mm x S32mm and for N = 2,250t x
0.4mm Cu dia wire in (3),
ML = 180mm.
µe = 1.0T x 10,000 x 180mm / ( 12.6 x 2,250t x 0.27Adc ) = 235.
(8) Calculate L for T32mm x S32mm, µe = 235.
L = 1.26 x 2.25th squared x 32mm x 32mm x 235 / ( 1,000 x 180mm )
=
8.5H.
(9) Calculate Air gap size, Ag.
µ max for close butted GOSS E+I, no real air gap = 1,000,
approximate.
Now it can be proved ( elsewhere ) that
µe = µ / [ 1 + ( µ x air gap in mm / ML of iron in mm ) ]
From this, Ag = ML x [ (1 / µe ) - ( 1 / µ ) ].
For T25mm core above, µ = 1,000, µe = 286,
Ag = 138mm x [ ( 1 / 286 ) - ( 1 / 1,000 ) ] = 0.34mm.
This the total gap, so the two gaps in ML each need gap material =
0.170mm.
Confirm Ag size when choke in use with 270mAdc.
The stack Smm does not make any difference to needed µe or Ag, but
stack height will
determine L and Bac which depends on Afe.
(10) Calculate Ag for T32mm core,
For 32mm x 32mm core, µe = 235, µ = 1,000, ML = 180mm,
Ag = 180mm x ( 0.004255 - 0.001 ) = 0.585mm,
Use gap material = 0.293mm, but confirm AG size when choke in use
with 270mAdc.
(11) Maximum Bdc should not exceed about 1.0Tesla for GOSS
chokes for CLC.
Max total Bdc+Bac can be 1.5Tesla for GOSS choke, so Bac can be up
to 0.5Tesla.
Ripple Vr frequency for full wave rectifier = 2 x mains F, 100Hz (
or 120Hz in USA. )
Bac = Vrms x 226,000 / ( Afe x N x F ), where 226,000 is a
constant.
Max Vrms = Bac x Afe x N x F / 226,000.
The 100Hz Vac across choke is approx = Vac at C1 - Vac at C2 and
where Vac at
C2 is less than 0.1 x Vac at C1, then Vac across L = Vac at C1.
For this example, Vac at C1 = 2.5Vrms.
Bac = 2.5V x 226,000 / ( 625sq.mm x 1,420t x 100Hz ) = 0.006Tesla.
This is a very small Bac, and Vac at C1 could theoretically be
198Vrms.
In most CLC rectifier filters, 100Hz Vac across the choke will be
less than 25Vrms
where Bac = 0.06Tesla, a tiny value, with means the Bdc could be
higher than
1.0Tesla.
Bdc could be 1.2T and ue would be 334 with smaller Ag. L would be
3.8H,
so the 100Hz attenuation factor increases, but only slightly. I
prefer Bdc = 1.0Tesla
to allow for where Iadc increases in class AB amp and for short
time operation
immediately after amp turn on.
(12) Tube rectifiers of any kind will arc internally and
then fail to become
useless if reservoir C exceeds values stated in data sheets for
the wanted Idc.
The data sheets also say what the series resistance should be
between HT
winding and tube diode. In old days, the HT winding always had a
CT taken to 0V,
so only 2 diodes are needed, and many rectifier tubes have 2
diodes with a common
cathode to suit the use, such as GZ34, one of the best I could
ever use for +420Vdc,
and OK for 135mAdc with C1 = 33uF.
but for 270mAdc, I would use 2 x GZ34 and 66uF or slightly less.
The Idc can double for class AB2, and to avoid the excessive peak
charge Idc,
the C1 can be kept at 33uF for the 2 x GZ34.
The Vac to Vdc conversion ratio with low reservoir C may be only
1.1 so for +420Vdc,
the HT winding is 420Vdc / 1.1 = 380Vrms - 0V - 380Vrms. Without
any load the B+
= +537Vdc, so all caps in CLC should be 350V rated but in series
pairs.
Thus the CLC filter could be C1 = 34uF 2 x 68uF in series,
L = 6.6H with T25mm x S50mm,
C2 = 235uF = 2 x 470uF in series.
100Hz Vac at C1 34uF = 0.27A x 2,200 / 34uF = 17.5Vrms. 100Hz
attenuation factor
= XC2 / XL = 6.8r / 4,148r = 0.0016, so 100Hz at C2 = 0.028Vrms =
OK.
Fo for 6.6H and 235uF = 4.0Hz = OK.
The RLdc = 420Vdc / 0.27A = 1,555r and time constant with C = 34uF
= 0.053Sec.
The Vpk-pk for C1 100Hz saw tooth wave = 17.5Vrns x 3.3 =
58Vpk-pk.
Where Idc is constant, the +420Vdc at C1 would fall to 0V in
0.05S, so this is
( 420V / 0.053S ) V / S = 7,924V / S and to reduce 58V the time =
58V / 7,924V = 0.0073S
This occurs during the time for each 50Hz 1/2 wave = 0.01S, so the
diode charges the
34uF for 0.73 of each 1/2 wave, so average charge current =
0.27Adc x 1 / 0.73 = 0.369A.
Average Ia for each diode of one GZ34 = 0.369A / 2 = 0.185A, and
peak Ia = 0.185A / 0.63
= 0.293A.
GEC data for 5AR5 = GZ34 peak Ia for each diode = 0.82A pk, so I
think what I propose
here is OK, but the GZ34 made now in China or Russia may not be
equal to what was made
in 1960.
The Vdc regulation with GZ34 will give PSU B+ output resistance of
about 200r.
So if Idc increases from say 270mAdc to 540mAdc, the Vdc drop =
-54Vdc, so you could
never get the 90W per channel; you could only ever get instant Po
of 90W.
In practice, when an amp is tested with pink noise that is
bandwidth limited to 20Hz to
20kHz, the peaks in noise waves will be seen to begin to clip when
average Po = 0.1
x maximum available instant Po, so 9W.
For hi-fi the GZ34 is OK until a tube loses its bias control and
draws much more Idc than
normal. 1 x GZ32 used to be used for 2 x KT66 but 1 x GZ34 are
needed for 2 x KT88,
and Quad-II-Forty used 1 x 5U4 which I sure did not like.
Choke input, ie LC filters with tube rectifiers works MUCH BETTER
than CLC because
peak diode currents are much lower. The regulation is better.
(K) Winding chokes.
Neat layer winding methods are best where patience, skill, and
machine lathes allow.
These days polyester-imide coated high temp grade 2 winding wire
is much more rugged
than fragile enamels of the past and wire can be wound on using
the "random winding"
method.
This means the wire is fed onto bobbin without layering neatly,
and turns are allowed to
pile up while slowly traversing the wire across the bobbin width.
This makes all the wire
crossings at a small angle so pressure between wires on wires is
not great. Wire is wound
with minimum tension, and varnish can be painted on every 200
turns so at the finish of
winding all turns are soaked in varnish. Towards the top of the
winding, hills and valleys
in the level of turns is minimised by feeding more turns into
valleys than on hills, so you
end up with height of winding that is all within 2mm of maximum
height.
Two pack epoxy slow set varnish is best.
After a final varnishing, wind two layers of flexible insulation
tape over all wire. Thus
arcing cannot occur between iron core and coil wire. Terminations
on the bobbin should
be provided where wire is less than 0.75mm dia.
People may find some old and useless transformer with an open
winding which may yield
a suitable amount of iron for a choke. Chokes in PSU do not demand
that the iron be top
grade GOSS. I often obtained E+I from re-cycled cores from fused
transformers.
The bell ends and bolts are all removed, and then whole
transformer is placed into a
small wood wood fire for 20 minutes and heat iron until just
cherry red hot. The heat
vaporizes and burns off any plastics and varnish. Next day when
the lams have cooled,
the E+I lams will all just fall out loose, and the heat will have
annealed the iron and won't
affect the iron's magnetic properties.
Unfortunately many people won't be able to light a fire anywhere
to fry old chokes and
transformers. But once the old iron is cooked the old wire can
easily be sawn through and
removed to a re-cycling bin. Don't try cooling hot cores in water.
Don't try to clean the
oxide layer off the laminations; it insulates the iron laminations
from each other which
prevents eddy current losses. If the material is not 25mm tongue
size, the turns and
current and wire size will have to be worked out to suit the
window size.
To Chokes 2
To Chokes 3
To Educational and DIY directory
To Index page


