LOAD MATCHING 2. SINGLE ENDED OUTPUT BEAM
TETRODES.
Last edited, 2017.
This page explains how to set up single ended output beam tetrodes
in tube amplifiers using the 6550
or KT88 working in pure class A beam tetrode mode with fixed Eg2,
In UL mode with OPT taps for
screens, or with local cathode feedback windings which are a
portion of the OPT primary winding.
Page content :-
Fig 1. Operation of the beam tetrode with cut-away sketch by RCA.
Fig 2. Ra curves for GE 6550A beam tetrode with screen at +200Vdc.
Tube properties.
Fig 3. Ra curves for GE 6550A beam tetrode with screen at +200Vdc,
loadline for class A RLa = 2k5.
Calculations and load line analysis steps. Comments about UL, CFB.
Fig 4. Ra curves for GE6550A beam tetrode with screen at +300Vdc.
Fig 5. Ra curves for GE6550A with Eg2 = +300Vdc, Load lines for 3
x RLa, 2k0, 4k2, 8k0, + analysis.
Calculations of THD reduction with NFB and Rout.
Graph 1. For power output for single 6550 beam tetrode vs anode
load value.
Choosing the OPT ratio.
Data for Ra, µ and gm for UL and comment on the effects of NFB and
distortion outcomes,
Rout calculated for complete amp.
Fig 6. Ra curves for 6550 in 40% UL mode.
Fig 7. Ra curves for 6550 in 40% UL mode with loadlines for 2k4,
4k1, 8k0.
Concluding notes.
-----------------------------------------------------------------------------------------------------------
Consider the the 6550 beam tetrode. This tube has four electrodes,
cathode, k, control grid, g1, screen grid,
g2, Anode, a, and two beam forming plates near the anode which are
each connected to the cathode.
Fig 1. Beam tetrode internals from RCA manual....
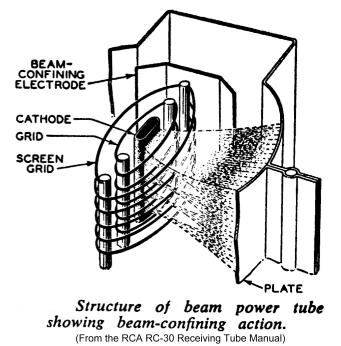
The sketch shows invisible electrons flowing from one side of
cathode to anode, but in fact electron flow occurs
on both sides of the cathode. The central cathode consists of a
flat metal tube and inside this tube is a length of
folded filament wire coated with a special inert insulating metal
oxide to prevent current flow from heater to cathode.
The filament has 3.5 ohms resistance when hot with an applied
6.3Volts at 1.8Amps needed to raise the temperature
of the cathode to about 900C. The small orange glow seen in tubes
is the hot central cathode. All other parts are
designed to run at a much lower temperature without any glow of
their own. The cathode, k, is often nickel and
coated with special metal oxides which promote the emission of a
cloud of electrons once the tube is warmed up.
This emission is only possible if there is a very pure vacuum
inside the sealed glass tube structure. The grid, g1, is
special fine wire wound in a slightly flattened helix with wires
spot welded to two support rods. All the grid support
rods, anode and cathode are supported in discs of inert mica
sheeting which rests against the glass internal glass
walls to locate all electrodes at their correct positions within
small tolerances, and keep the assembled structure
stable without vibrating. The pitch and size of the helical coil
and and its distance from the cathode and anode
determine the tube behavior.
Grid 1 is usually set up with a bias dc voltage about -50Vdc below
the cathode potential. By varying the grid 1
voltage + and - with an ac signal, the flow of electrons from
cathode to anode is controlled fairly linearly.
The grid 1 draws no current because its negative charge repels
negatively charged electrons.
There is a second grid of larger size, screen grid, g2, placed
between grid 1 and anode. Its helical coil wires are
aligned to the g1 wires to allow electrons flowing past g1 to also
flow past g2 wires to flow to anode.
Screen g2 usually has a potential at +300Vdc above the cathode and
it attracts and absorbs about 10% of
electrons flowing, leaving 90% to flow to anode to be absorbed.
The electrons arriving at screen generate heat about equal to 1/15
of the heat generated at the anode.
The TWO beam forming plates are connected internally and
permanently to the cathode, and create regions
on each side of cathode where the positive charge of anode is much
less, thus focusing electrons into
two beams, one from each side of cathode.
The increased density of electrons suppresses the effect of
electrons bouncing off the anode and returning
to the next best positive thing, the screen, and the electron
bounce is called secondary emission.
The beam forming plates were invented to counter the need to pay
royalties to European based company
Philips who had invented the pentode which has a third grid, g3,
between screen and anode which functions
similarly to suppress secondary emission electrons bouncing off
anode to then go to screen.
The action of screen in the first early tetrodes gave a queer
shaped set of anode curves which involved a region of
positive Ra which could cause high THD or oscillations. The
suppressor grid or beam forming plates make the pentode
and beam tetrode become one of steps towards a world with
efficient radio communication and audio amplification.
The plate, or anode as it should be called is a sheet metal box
with open ends and it absorbs about 90% of the
electrons emitted from the cathode with the balance of 10% being
absorbed by the screen.
The presence of a more positive anode with respect to cathode
means that metal atoms have an absence of the
full number of electrons in the concentric orbits around the
atomic nucleus of protons and neutrons.
In other words, an anode has atomic holes for electrons to fill.
The voltage of anode exerts an electrostatic
field force to all things around it. The field intensity is
highest near the anode, but declines with square of
distance away from anode. Negatively charged electrons swarming
around the cathode are attracted
to anything positive and the flow of electrons is altered by the
combined effects of voltages at grid1,
screen grid 2, and anode.
The anode has open ends to allow some heat to radiate from the
cathode more easily up and downwards.
Much of this is blocked by mica plates to hold electrodes. Most
heat generated by activity in the confined volume
between anode and cathode is radiated away by the outside metal
surface of anode and through the glass to outside
world. The glass absorbs some heat and the common limit on its
temperature is 250C. Higher temp will cause glass to
melt, and deform to let air into tube which puts an end to the
tube's life.
The anode is heated by the flow of electrons and its heating is
known as its plate dissipation, Pda, easily calculated
as Pda in Watts = Ea x Ia, ( Volts x Amps ). Screen heating is
calculated Eg2 x Ig2.
With no signal, idle heat in any at anode = Eadc x Iadc, but this
can vary when signals are present.
The total tube heat in a pentode or tetrode = Pda + Screen Pdg2 +
cathode heating. Data for Pda does not include
cathode heating, but the data figures include for it already.
The silver coating on the inside of the glass is called gettering,
a very thin layer of special metal which absorbs stray O2 and N2
air gas molecules to form oxide or nitride
compounds which are then locked to the glass rather than
re-cycling around the tube and increasing accumulatively,
and destroying its operation.
The advantages of the beam tetrode and power pentode allow for
about twice the audio or RF output power to be
generated when compared to triodes of the same size and cost of
production and same anode dissipation.
While such a feature is extremely useful, it is also useful to
operate the tube with its screen connected to anode to
make the tube operate as a triode which has lower Ra and less THD
than when used as pentode or beam tetrode
with a fixed Eg2.
For 6550 or KT88, maximum anode dissipation Pda rating is 42W, and
the theoretical maximum amount of
audio power from a single tube in class A1 = 18W in beam power
mode, but only about 10W in class A1 triode.
In practice, nobody should ever have a single 6550 set up with
idle Pda = 42W, say Ea = 400Vdc with
Ia = 105mAdc. The tube would seem to run too hot, and it will have
a short life. I recommend idle Pda max for
all pure class A operation = 0.7 x Pda rating, so for 6550 that
means 29.4W, and say +400Vdc x 73mAdc for Ia.
Ig2 could be 6mA, and with Eg2 = +400Vdc, Pdg2 = 2.4W. So the
total Pda+g2 = 31.8W. For class AB operation
I recommend maximum idle Pda+g2 = 0.6 x Pda rating, 25.2W. In many
PP AB amps I have used idle Pda = 17W;
tubes then last twice as long as with Pda 29W, and surprisingly,
the sound remains fabulous.
But for SE amps, let us stay with max Pda 29W for 6550. Max anode
Po in beam tetrode, UL or CFB mode will
be about 0.43 x Idle Pda = 12.5W. Some Po will then be lost in
winding resistance of OPT. If that is 7%, expect
SE max Po = 11.6W, so actual anode efficiency = 100% x Po at sec /
Pda at idle = 100% x 11.6W / 29W = 40%.
If all we want is 10W, tube idle power = Po / 0.4 = 10 / 0.4 =
25W.
Most 6550 are now supplied by New Sensor Corp and USA joint
venture with Russian factories. There are various
brandnames, Electro Harmonix, EH, Tungsol, to replace Sovtek,
which was the Russian factory name going back
to time of USSR before 1990s. The working characteristics of these
recently made Russian tubes appear to be
equal to NOS samples of the same tube type such as the renowned
GE6550A, MOV KT88, although it seems to me
EH6550 and EHKT88 have exactly the same internal structure. The
properties of the EH6550 has been dealt with
extensively at my page at basic-tube-4.html
In 2011 I found Russian 6550 or KT88 have data parameters of Ra =
19k0, µ = 190, gm = 10mA/V at Ea = +400V,
Ia = 90mA, and Eg2 = +350V.
This is at Pda = 36W. In class AB amps, SE 6550 or KT88 are set up
with Ea = 450V, Ia = 51mA, for Pda = 23W,
giving Ra = 32k0, Gm = 5.5mA/V, µ = 176. This is very different to
data quoted for the higher Pda condition which
causes Ra to be lower and Gm to be higher.
Therefore setting up SE 6550 with Pda 30W with Ea = 400Vdc, Ia =
75mAdc will give figures intermediate to
36W or 23W. Anode curves for GE 6550A are similar to EH6550.....
Fig 2. Ra curves for GE 6550A with Eg2 = 200Vdc.
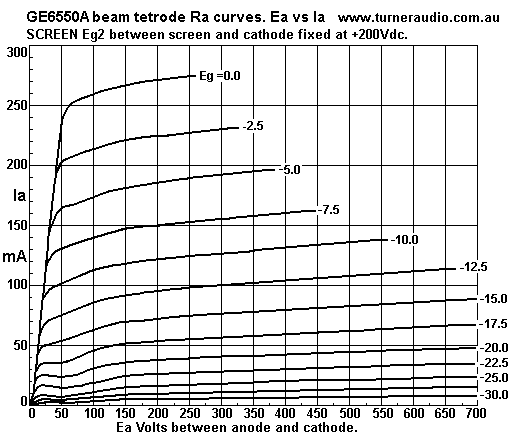
Fig 2 curves are for GE6550A but are typical for any 6550 made
now. If we look along the Ia = 100mA line
we see that for a change of Ea from 300V to 650V, the Eg1 will
change about 1.5V, µ = 350 / 1.5 = 233.
For the same 350 change of Ea with a fixed Eg1 = -12.5V, Ia
increases 15mA, so Ra = 350V / 0.015 = 23.3k.
Eg1 changes from -12.5V to -10V, the Ia change is 26mA at Ea =
300V. Therefore gm g1 = 26mA / 2.5V
= 10.4mA/V. The Ra curve at 100mA for Eg1 -12.5V is fairly
straight, and we should be able to say can say
µ = Gm x Ra = 0.0104 x 23,300 = 242. This is not 233 as above, but
we are close, and you can see that Ra
curves are rather unevenly spaced and Ra and gm and µ varies a lot
at different points on the data sheet.
The anode curves are more crowded together at the bottom of graph
and this shows Ra is higher and gm lower
at lower Ia levels which are most commonly used in most amplifiers
for 95% of the music energy. From such
curves it is impossible to predict THD spectra accurately, but we
can assume there will be a lot of THD no
matter what load is used or where the idle Q point is.
Fig 3. GE6550A, class A RLa 2k5, Eg2 = +200Vdc.
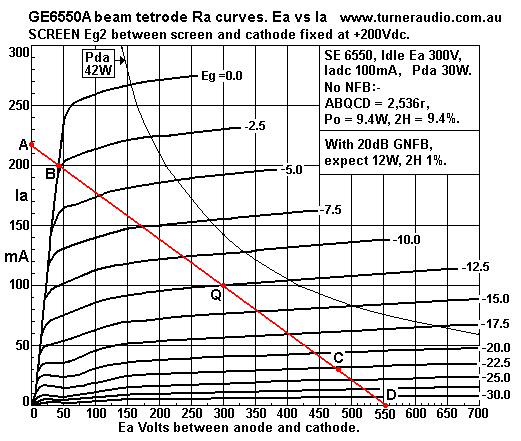
The SE 6550 has idle Pda = 30W, and has class A SE load of 2.54k
which can yield up to about 12W
at 1% THD but only if there is a total of 20dB NFB. Without any
NFB, THD has 2H and a many other
H of significance. Damping factor = poor = 0.108. The first 3W
offer fair linearity.
Calculation of load will give approximate SE anode load RLa = 0.9
x Ea /Ia at idle = 0.9 x 300V / 0.1A
= 2.7k. Pda = 30W at idle.
Plotting the SE class A1 load line on Ra curves for 6550 beam
tetrode, Eg2 = 200V:-
The load I show was simply worked out graphically:-
1. Choose position of point Q. The curves indicate the idle Ea can
be +300V, and with idle Pda = 30W,
the idle Iadc can be = Pda / Ea = 30W / 300V = 100mAdc. Plot point
Q at "co-ordinates" of 300V x 100mA.
2. Plot B on diode line and at 2 x idle Iadc, at 47V x 200mA.
3. Calculate the maximum theoretical negative going Ea swing = Ea
at point B - Idle Ea = 47V - 300V
= -253Vpk.
4. The maximum theoretical positive going Ea swing must be equal
to the negative swing, and is result of tube
Ia reducing to 0.0mA. Therefore max Eapk = Ea + max swing = 300V +
253V = 553Vpk.
Plot point D at 553V x 0.0mA.
5. Draw the SE class A load line from point D to B and on to Ea =
0V axis, and plot point A.
6. Read off the positive going Eg1 swing between Q and B = -12.5V
to -2.45V = +10.05V.
7. Calculate negative peak Eg1 swing assuming Vg applied is
linear, and +/- Vgpk swings are equal.
Max Vg1 negative swing = -12.5V - 10.05V = -23Vpk.
Plot point C on line ABQD at Eg1 = -23V.
8. ABQCD is the completed load class A SE load line.
Calculate its resistance load value = maximum theoretical +/- Ea
swing / +/- max theoretical Ia swing
= 253V / 100mA = 2,530r.
9. Alternatively, calculate RLa = max Ea / max Ia on both axis, =
553V / 218mA = 2,536r.
10. Calculate Po without NFB. The peak to peak Ea difference
between B and C = 47V - 476V
= 429Vpk-pk.
The approx Vrms applied to load = Vpk-pk / 2.83 = 429 / 2.83 =
151.6Vrms.
Po = Va squared / RLa = 151.6 x 151.6 / 2,530r = 9.08W.
11. Where BQ distance is not equal to QC, Calculate 2H = 50% x (
253 - 177 ) / ( 253 + 177 ) = 50% x 76 / 430
= 8.8%.
Note, there may be considerable 3H and other H present.
12. Calculate maximum possible theoretical Po where THD is reduced
by NFB to < 0.5%.
Po max possible = 0.5 x Iadc squared x RLa = 0.5 x 0.1A x 0.1A x
2,530r = 12.65W.
Note, 20dB NFB could theoretically reduce THD by factor = 0.1, ie,
from 8.8% to 0.88% at Po = 12W
approx, slightly under the theoretical max Po which is only
possible with a perfect tube which was never ever
created.
13. Estimate the Ra at low levels of operation.
Read off the Ia change on Ra curve for Eg1 = -12.5V, and for +/-
100Vpk each side of Q.
Total current change = 8mA for 200V Ea change. Ra = Ea change / Ia
change = 200V / 8mA = 25k.
14. Estimate the grid g1 gm for a small portion above and below Q.
Read along vertical line through Q for Ea = 300V. For Eg1 change
of +2.5V, Ia change = +28mA, For Eg1
change of -2.5V, Ia change = -25mA, so for total Eg1 change of 5V,
there is Ia change = 53mA,
and gm = 53mA / 5.0V = 10.6mA/V.
15. What is the amplification factor µ at Q? µ = Gm x Ra =
.0106A/V x 25,000r = 265.
16. What is the gain with RLa shown, and without NFB ? Gain at max
Po = max Vrms for RLa / max applied
Vg rms = 151.6Vrms / 7.1 = 21.35.
What is the gain at low levels? For Eg1 swings of +/- 2.5Vpk, Ea
change is from 234V to 351V
so gain = 117Vpk-pk / 5Vpk-pk = 23.4.
Note the gain at low levels is higher than at max level because of
change of gm and distorted transfer function
at high levels.
17. The THD for SE pentodes and beam tetrodes has varying amounts
of mainly 2H and 3H, but with many
other H so that load line analysis can only ever be approximate,
and trying to forecast the exact THD outcome
is a complete waste of time. But we can say that THD produced by
SE pentodes and tetrodes is "bleedin awful mate",
and we should strive to set up such tubes using CFB, Triode, or
UL, in about that order of effectiveness to get
the tube to make much less THD without reliance on GNFB.
18. The OPT should have primary RLa = 2k5, +/- 15%, and sec load
matched for 4r0, 8r0, 16r0.
The Ea can be slightly higher and Iadc lower for slightly higher
RLa, and Ea lower with Iadc higher for slightly
lower RLa.
The load match has been found for the SE 6550.
Other considerations,
The Damping Factor without NFB is extremely poor, and = RLa / Ra =
2.53k / 25k = 0.102. However, the use
of 20dB of NFB will increase the DF to more than 8.0.
The 20dB NFB may consist of GLOBAL NFB, ( ie GNFB, ) in one loop
from OPT sec to an input tube cathode,
or it may consist of local NFB in an output stage of up to 12dB
plus a balance of additional GNFB.
A good form of local NFB in an output stage for a tetrode or
pentode is CFB, cathode FB, and has say 20%
of the turns of OPT primary between cathode and 0V, and with 80%
between anode and B+. This is called output
stage CFB, and Quad called this The Acoustical connection. This
amount of NFB will be found to reduce tetrode Ra
to be Ra' ( with local NFB ) = tetrode Ra / ( 1 + [ ß x µ ]),
where ß is the fraction fed back, and µ is amplification factor
and the screen is bypassed to the cathode. We should get Ra' =
25,000r / ( 1 + [ 0.2 x 265 ] ) = 463r, which is less
than 1/2 the Ra of a triode connected 6550 at the same Ea Ia
conditions.
The use of a 50% UL tap will also reduce Ra to around 2k5, and is
equivalent to about 4.5dB of GNFB.
This is a mild amount of NFB, and if UL tap is moved to anode, the
6550 is triode connected, giving Ra about 1k0,
equal to 6dB GNFB.
I found superlative results with 20% CFB but with screen bypassed
to 0V, so the tube operates as if it has 20%
UL taps, but also has the 20% CFB in grid circuit. see 35W SE and SE32
amps.
NOTE. Pure beam tetrode and CFB can use fixed Eg2 = 2/3 Ea but for
UL, the g2 is at same Vdc as Ea, +300V
because OPT primary has low winding resistance. Thus the -Vdc bias
for grid is high for UL, ( or triode ) or where
Ea = Eg2. The lower Eg2 allows for lower grid bias. The Ra curves
will much change their shape with change of
Eg2 and Ra, µ, gm and THD will all change. But for the same idle
Ea and Iadc, Po will remain about the same.
Fig 4. 6550 tetrode Ra curves for Eg2 = 300Vdc.
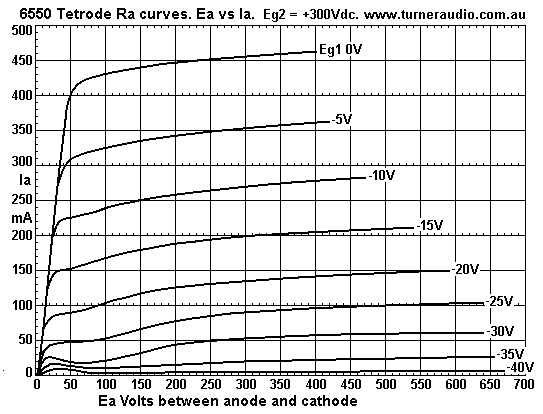
Fig 4 shows overall similar shapes for Ra curves, and is like Fig
2, but the knees of Ra curves for Eg1
values are higher, which allow the tube to give a higher maximum
Iapk. Notice that the knee of the Ra curve
for Eg1 = 0V is at 50V x 400mA. The slope of diode curve = 125r.
In Fig 2 for Eg2 = +200V, the knee is at
55V x 245ma with diode curve R = 224r. In samples of 6550 I have
tested, the diode line slope may not reach
the low resistance indicated by curves. With 50% UL connection or
CFB use, I always have allowed diode
line for most beam tetrodes and pentodes being 280r and if it is
lower, then measured results for Po may be
higher than estimates with 280r predict, which would be a bonus.
In practice, the lowest Rd diode line resistance is with pure
tetrode. But with UL or CFB, the Rd will increase,
and there is some variation in tube samples.
Fig 5. 6550 tetrode, Ea +350V, Eg2 +300V, RLa 2k0, 4.167k, 8k0.
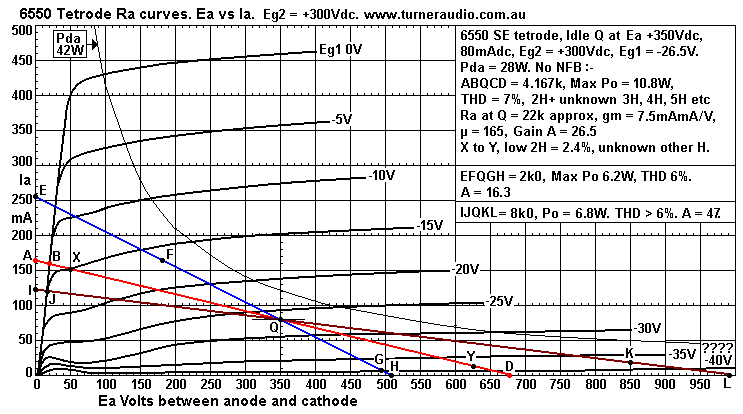
Fig 5 shows 3 loads of SE 6550 tetrode. ABQCD is loadline for PURE
CLASS A and it gives the
highest amount of pure class A Po. It is 4.167k and plotted with
point B at twice idle Iadc on diode curve,
and all points have been plotted similarly to the 2k5 load in Fig
3.
RLa load for max Po is calculated RLa = 0.9 x Eadc / Iadc = 0.9 x
350V / 80mA = 3.937k. This is close to
loadline result, only 5% lower than 4.167k.
For load RLa = 4,167r the theoretical max Po = 13.3W and with Ia
swing = +/-80mApk, and Ea swing
= -/+330Vpk. Symmetrical clipping occurs. Theoretical max Po
assumes enough NFB is used to get
THD < 0.5% at clipping.
As clipping is approached, THD spectra increase, and the THD
amplitude The NFB reduces levels of all
THD but will add a few more H due to intermodulation effects. But
a typical SE tetrode or pentode may
make 10% THD near clipping, and the 20dB NFB reduces this to not
less than 1%. The THD % is roughly
proportional to the output Vac. If max Po = 12W, and the tube
makes 1.2W, Vac level is about 1/3 of the pull
power level and THD with NFB is 1/3 of the 1% at 12W, ie, 0.33%,
and this cannot be ignored. The amounts
of 2H, 3H, 4H, 5H are the majority, but the relative amounts
cannot be estimated by load line analysis. The THD
of tetrodes and pentodes has always been considered to be worse
than triode or UL connection.
Tetrodes and pentodes have high 2H when RLa is very low or very
high, and there is a load where 2H is
extremely low, but where 3H and
others are high. And the phase of the 2H with low loads is
opposite to 2H phase at high loads. So that you
cannot avoid ever high THD. I spent considerable time plotting THD
vs Va for 6550 at my page at basic-tube-4.html
There are numerous graphs for THD vs Va for many idle Ea and I
conditions, and comparisons to triode connection
of 6550. In general, all tetrodes and pentodes must have high NFB.
For the 6550 with idle Ea 350V x 80mA, the OPT can be 4k0 : 4r,
8r, 16r.
If the OPT has total input winding resistance = 10%, then the
input load becomes 4k4. Speaker loads vary so
much with frequency that the anode load may vary between 3k and 9k
and. All amps have to deal with this
problem, so all must produce useful output and remain stable for
this load range.
I would never use any beam tetrode or pentode in pure single ended
mode with fixed Eg2 and no local CFB,
or UL tap.
If no winding arrangements for UL or CF are possible with an
existing OPT, I always preferred to use a
triode connected tetrode or pentode. In many old AM radios with a
single 6V6 or 6BQ5 and with negligible
if any NFB, I was able to reform the PSU for a higher B+ and
better hum filtering and then replace the 6V6
or 6BQ5 with an EL34 in triode with the same OPT. The output power
is much increased, and with NFB
the sound usually doubles, and the sound becomes hi-fi instead of
glorified noise. Triode connection is the
fall back position where suitable arrangements on OPT are not
available to improve linearity. The LOAD
ratio of OPT meant for 6V6 o 6BQ5 was often just right for EL34 in
triode. Even in an old radio,
load matching is very important.
The effect of GNFB on gain and on THD of any amp may be calculated
where there is NFB from speaker
output Vo to cathode of an input tube :-
Gain with NFB = A' = A / ( 1 + [ A x ß ] ), where A = gain
without NFB, ie, Vo below clipping / Vg-k of
input tube. ß is the fraction of Vo which is applied to input tube
cathode, and 1 is a constant to make the
equation work every time.
Example. Amp makes 10W into 6r0 speaker load = 7.75Vrms. The Vg-k
needed without NFB = 0.07Vrms.
Gain A = 110.7.
Let us say ß = 0.08. Then 0.62Vrms is applied to cathode of input
tube.
Then Gain with NFB = 110.7 ( 1 + [ 110.7 x 0.08 ] ) = 11.23.
The Input Vac between V1 grid and 0V = 7.75Vrms / 11.23 =
0.69Vrms. which are in series and sum to
give 0.69Vrms input Vac.
The gain is reduced by factor = 11.23 / 110.7 = 0.101, and the
applied NFB = 20dB. THD is reduced by
the same amount, and output resistance is reduced by a higher
factor.
If Dn at 10W = 7%, expect Dn' = 7% / ( 1 + [ 185 x 0.0486 ]
) = 0.7%. If the Dn at 1W = 2%,
Dn' = 0.2%, and probably amp may sound OK.
The amount of NFB in dB due to FB is 20 x log (A / A') = 20 x log
(185.3 / 18.53 ) = 20dB
If there was no load at the OPT secondary, the loading of the tube
becomes the primary winding reactance
which may be 40H at 20Hz, reactance = 5k0 but at 1kHz the XLp
could be 50k. The gain of output tube
may increase 10 times, and then the total A of the amp increases
10 times, and the amount of applied NFB
increases by +20dB, so NFB with no load may become 40dB
instead of 20dB when correctly loaded.
With such a high possible increase of NFB where RLa is not
connected, or load has a high value at some
frequencies, the amp is 100% likely to become unstable at LF and
HF due to unavoidable phase shifts so
the gain must be reduced with zobel networks and critical damping
networks similar to what is found elsewhere
at this website in nearly every amp I have detailed in countless
schematics.
The calculation of output resistance is more difficult to
calculate because we are need to take into account
the µ of the output tube. To reference our calculations to the
secondary connection, µ' of the output tube at
the OPT secondary = tetrode µ / OPT turn ratio. In this case
for 6550 with 4k0 : 4r0 OPT, TR = 31.62,
so µ' = 265 / 31.62 = 5.22.
The output resistance, Ro' with GNFB of a tube amp can be
calculated if you know :-
1. Voltage gains of the input and driver stages, nominated as A".
2. µ of the output tubes between g1 and anode.
3. ZR of OPT.
4. Turn ratio TR of primary to secondary which is the unloaded
voltage ratio between P and S windings, ie,
the square root of the P : S load ratio.
5. Anode resistance, Ra of output tube or tubes at the Q point.
6. Total of winding wire resistance total Rw of the primary and
secondary windings of the OPT looking into the
primary anode terminal. Allow total Rw = 10% for an SE OPT.
7. ß, fraction of Vo at sec fed back to input.
For example, let us consider the 6550 in pure beam tetrode mode in
Fig 5. It is driven by driver triode and
input triode with their gain
1.A" = 100.
2. µ of output tube = Ra x gm = 25,000r x 9mA/V = 225.
3. ZR of OPT = 4,167r / 6r ) = 694.5.
4. TR = 26.35.
5. Ra = 25,000r.
6. Total Rw at OPT primary input = 417r.
7. ß = 0.1
Calculate Rout of the SE amp with 6550 tetrode with 20dB GNFB
applied :-
Ro' = ( Ra + total Rw ) / ( ZR x { ( 1 + [ A"
x µ x ß ] / TR } )
= ( 25,000 + 417 ) / ( 694.5 x { 1 + [ 100 x 225 x 0.1 ] / 26.35 }
)
= ( 25,417r ) / ( 694.5 x [ 1 + { 2,250 / 26.36 } )
= 25.417 / 86.36 = 0.2934r.
If RL at amp sec = 6r0, then DF = 6.0 / 0.294 = 20.38, which is
very good, and indicates we may be able
to reduce the amount of GNFB by reducing ß to a lower value of
probably 0.07.
I leave you to compose the schematic fully and work it all out
again. Then build the amp, and see if your
measurements agree with the calculations.
Use of UL taps between 40% and 55% for SE 6550 will give nearly
same Po as pure tetrode maybe 11W
max, and triode connection would give about 9W output. The
calculations for Ro use the same above formula
but the Ra and µ for UL or triode must be worked out.
-----------------------------------------------------------------------------------------------------------------
Graph 1. Po vs RLa, SE 6550 beam tetrode.
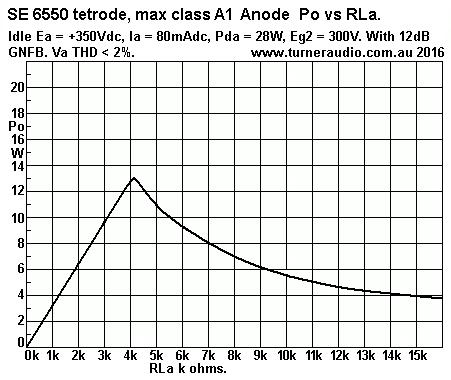
The power levels are for low THD < 1%, just under onset of
clipping, with 20dB GNFB. Po has been calculated
for Ra curves in Fig 5. There is at least 7W available for all
loads from 2k3 to 7k8. If the OPT has 4k2 : 6r0 ratio,
all loads between 3r3 and 11r1 will be tolerated providing
output power average is kept below about 0.5W.
If two amps for stereo make 1.0W total, SPL = 90dB average = very
loud using speakers rated for 90dB/W/M.
Many ppl I met needed only tiny average power levels yet they
insisted on amps capable of 100W per channel,
which is usually quite absurd.
Single Ended Ultralinear could be another option to use.
Fig 6. The graph here is for a GE 6550A with 43% screen taps.
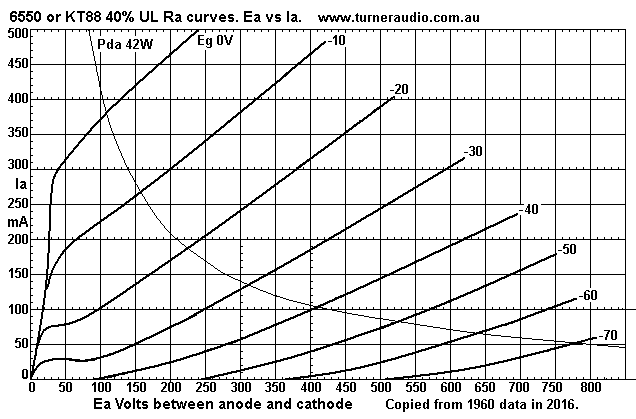
One glance at these curves should tell you they look very
different to triode or tetrode curves, and in fact are
intermediate between the two because 40% of the anode Va is
applied to screen g2. Some loading of OPT
occurs at screen tap because the screen has Vac and Iac input, a
few k ohm, and there is some loading of anode;
but it is over 10k, and we may neglect it.
The 6550 model for UL 6550 or CFB is now more fully explained at basic-tubes-4a.html
The 40% UL tap tidies up the ragged behavior of pure beam tetrode
especially at extremes of peak Va swings.
The THD of 40% UL becomes almost equal to triode, and with less
odd number H. The diode line on far left
shows Rd < 125r until 300mA. But above this Ia, the Rd rolls
right with line for Eg 0V at about 900r.
This indicates there is zero -Va swing limiting by any load line
at peak Ia = about twice Iadc at idle.
The Ra curves indicate that in class AB push pull operation where
the RLa-a is low, Ia could not swing up to
430mApk where PP RLa-a = 4k5 and where a pair of KT88 could
generate 100W with Ea = +600Vdc.
The curves are digitally tidied up copies of 1960 curve data, and
are accurate enough to be a useful guide to
use of UL taps to make operation much better than pure tetrode for
hi-fi amps.
Fig 7. 40% UL curves, RLa loadlines for for 2k4, 4k1, 8k0.
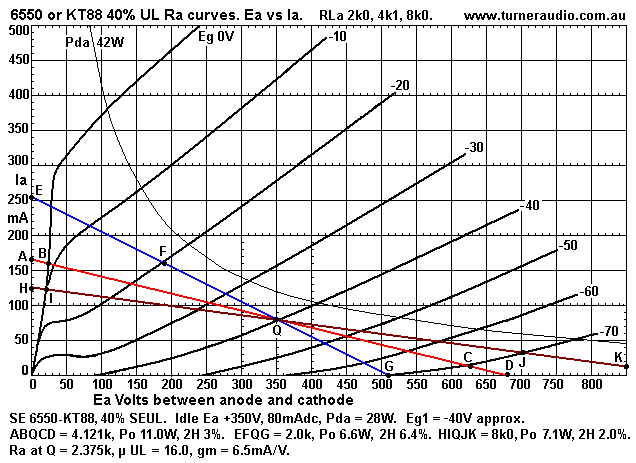
SEUL reduces THD to being like triodes, and cleaner, and SE load
calculations are the same as for beam
tetrode mentioned above for Fig 5.
The load for max SEUL Po is 4k1, so OPT could be 4k0 : 4r0, 8r0,
16r0, or more simply 4k0 : 5r0 which
suits all loads above 3r0. The Po vs RLa graph for UL will be the
same as Fig 5.
CFB works extremely well in SE amps. See my best examples of CFB
use in SE35W monobloc
amps
with 4 parallel EL34, and in SE32W
monobloc amps with 1 x 13E1.
You are at
LOAD MATCHING 2,
SE BEAM TETRODES + PENTODES
Back to LOAD MATCHING 1,
SE TRIODES
Forward to
LOAD MATCHING 3, PP
TRIODES
LOAD MATCHING
4A, PP TETRODES and PENTODES
LOAD MATCHING
4B, PP TETRODES and PENTODES
LOAD MATCHING
4C, PP TETRODES and PENTODES
LOAD MATCHING 5
about beam tetrodes
To Educational and DIY
Back to Index Page 

