TUBE
OPERATION 1
SMALL SIGNAL AMPLIFIERS, edited 2017.
Contents :-
Some history of triodes and basic tube operation of cathodes,
anodes and grids.
Fig 1, Vacuum diode internal structure, A, B, C show basics of
tube diode Ia flow.
cathode emission and electron flow explained.
Fig 2, 5AR4 diode Ra curve for one of its diodes.
Fig 3, Internal structure of typical triode. Schematic for the
electrodes.
DC flow for quiescent conditions, dc equilibrium, interactive
effects of anode voltage
and grid voltage on electron flow. Effect of cathode bypassing
biasing on Ra, and gain.
Ra explained. Complex and easy way to measure Ra.
Fig 4A, schematic for measuring Ra of twin triodes µ and gm
explained and how to measure
and calculate them.
Measure 1/2 12AU7, steps 1 to 8.
Fig 4B, PSU for schematic in Fig 4A.
Fig 5, Basic electron flow in 1/2 6SN7 small signal amp. About
internal operation.
Fig 6, Basic schematic of 1/2 6SN7 preamp stage DC operation of
1/2 6SN7.
DC flow, calculation of Rk for cathode biasing.
Fig 7, Voltage Generator Model of 1/2 6SN7. Measuring triode
output Vac and effects
of meter impedances. NFB in triodes.
Fig 8, Current Generator Model of 1/2 6SN7 with grid and anode
transconductance
explained.
The paradox of NFB in triodes, how to support the idea of Negative
Feedback within
every triode. Shunt C and Miller effect.
Pentodes vs Triodes
Fig 9, internal construction of pentode.
Fig 10, 6AU6 in simple amp model.
Fig 11, Schematic of 6AU6 using Current Generator model and with 2
shunt NFB loops.
----------------------------------------------------------------------------------------------------------------
The history and operation of vacuum tubes is best described in
many of the old text
books that one might still find in university reference or archive
libraries providing you
don't mind the smell of old books stored in the basement. Many
institutions have thrown
out many of their old pre-1960 books which are no longer read by
anyone, and security
arrangements prevent access to anyone wanting to spend time for
days reading and
photocopying valuable information, or wasting resources on copying
silly old ideas about
obsolete vacuum tubes. I can only give a very brief description of
basic operation for the
common tubes we may have used since 1928 to present day in audio
amplifiers.
My favorite book of vacuum tubes is Radiotron Designer's Handbook,
4th Ed, 1955.
It was written in a spirit of altruism, to get more people to
understand electronics for radio
reception, audio amps, and recording on disc. RCA funded its
production team and made a
handsome profit in increased tube sales.
The first vacuum tubes were called electron valves, because this
referred to the way
these electronic devices controlled current flow rather like the
flow of a fluid or gas in a pipe
is controlled by turning a tap handle using low power of a hand to
alter the pipe flow which is
delivering much higher power to some device.
The first simplest "Valve" was a diode with only two electrodes
called anode and cathode
and mounted inside a sealed glass container which resembled a
simple light bulb.
The two electrodes are kept a small distance apart, perhaps 1mm to
10mm, and all air was
extracted to leave a good vacuum within the bulb.
An early diode from 1920 has the bulb with THREE terminals, two
for each end of a thin
cathode wire and one for the anode.
The cathode is by far the most complex item within every vacuum
tube, mainly because
of the chemistry needed to alter the properties of raw metals like
nickel or tungsten to be
able to emit far more electrons than if they were used without the
added chemistry.
All cathodes must be heated to between say 800C and 2,500C for get
the metal atoms
excited enough to allow electrons to exit orbits around atom
nuclei.
Cathodes are either directly heated, DH, or indirectly heated,
IH.......
DH cathodes are used in 5Y3, 5U4, 45, 300B, 845, and are a length
of wire folded to a
shape and requiring a DC or AC current flow from one end to other.
5Y3 needs 5V x 2.5A
or 7.5W to heat its cathode, 300B needs 5V x 1A, 845 needs 10V x
3.3A.
The red heat cathodes have barium carbonate and oxide coating of
nickel alloy wire, 845
has tungsten wire doped with thorium which impregnates the
tungsten surface. The tungsten
runs at white heat above 2,000C. The most delicate DH tubes were
used in portable radios
which needed 1.4Vdc x 100mA.
IH cathodes are found in GZ34 diodes, and countless other triodes
et all, such as 6V6,
12AX7 etc.
The cathode is a metal tube with circular or rectangular section,
and coated with barium and
strontium carbonates or oxides on the outer surface. Inside the
tube there is a folded tungsten
heating filament wire coated with non emissive oxide to keep it
insulated from cathode.
Heating power of 6.3Vac or Vdc between 0.15A to 3A is applied red
heat at cathode of above
800C. Such a cathode was invented in 1930s which allowed radio
tubes in countless radios to
heated by a Vac winding on mains transformer. At the time, mains
Vac power was becoming
available to ppl in many cities around the world, and expensive DC
power from batteries was
becoming obsolete. The IH cathode was much more rugged than the
DH. If you drop a 300B,
and don't break the glass, you may break the cathode wire. But you
could drop a 6550 many
times without ever breaking anything, providing you don't break
the glass.
Just try to be careful with all tubes; do not break them open
without a gas mask and goggles
and first wrapping them in a cloth bag to prevent glass spraying
around and to prevent toxic
chemicals reaching your air ways or mouth.
The hot metal cathode generates a cloud of millions of electrons
around itself while operating
in a vacuum. Heated metal atoms give electrons higher energy and
some spin away from the
metal atom where they are like stone thrown in the air,
which lose kinetic energy during their
flight away, then try to fall back to hot metal and maybe repeat
the process endlessly. Electrons
return to orbits of atoms which are available and free of an
electron. One might assume some
atoms take in an extra electron, while some atoms lose an
electron. But unless electrons
migrate to some other electrode there is no current flow and the
charge at cathode is the same
as the point to which the cathode is connected.
The electrons swirling around in cloud around cathode is called
the cathode "space charge",
and is invisible. The electrons emitted into cloud all have a
negative charge, and tend to repel
each other and limit the number of electrons which gather around
the cathode, so the space
charge stabilizes in a state of equilibrium if there is no outside
influence on the charge.
But where there is a positive anode say 5mm away from space charge
electrons, there is a
force on all electrons to want to travel to anode. The force
varies, so a fair number can be
enticed to travel to anode instead of returning to cathode and
this causes a deficit of electrons
in space charge so more electrons are immediately emitted to
replenish the loss of those
travelling across the vacuum to anode. The cathode attracts
electrons from the negative
terminal of a B+ power supply, and the positive anode absorbs the
electrons and sends them
on to positive terminal of B+ Power supply.
Thus you have a current which flows around a circuit and heat is
released at a rate of V x I in Watts,
and this will drain the stored charge in a battery or consume
power from a Vac transformer winding
when the peak +Voltage causes current to flow. The direction of
electrons can be only one way in
all vacuum tubes. If the anode becomes negative below cathode
voltage, no current will flow.
So the diode can be used to allow current flow on positive going
peaks of Vac waves while not
allowing any current on negative going peaks of Vac waves. This is
an extremely valuable
property of all diodes.
Quantum physics explanations or formulas are not found at this
website. If you wish to
know more, then study elsewhere, but you'll need to understand
formulas which go from
one side of PC screen to other, with a dozen or so items which
themselves take a week
to understand. But you do not need to know everything about
sub-atomic particle properties
to build fabulous amplifiers with tubes or transistors. The cloud
of electrons around a cathode
is called a "space charge" and is mentioned in books such as
Radiotron Designer's Handbook.
Tubes are quite easy to understand well enough to use them
optimally. Transistors are also
easily usable after basic knowledge but hardly anyone knows just
exactly what is happening
internally.
The anode is a metal plate or tube or box surrounding a cathode.
It is not intended to run hot,
but is heated by radiated heat from cathode, and by action of
electrons arriving at its surface
and absorbed by the metal. The anode usually runs below 250C.
For electrons to flow across the vacuum from cathode space charge
to anode the anode
must have a positive charge in respect to the cathode. This may be
done using a battery
with + terminal to anode, -terminal to cathode.
Fig 1. Vacuum diode.
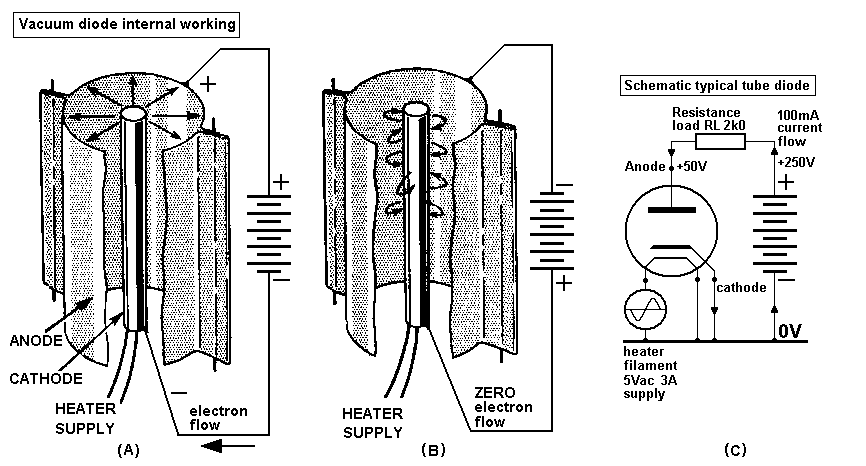
Fig 1 shows a very basic diode which has an indirectly heated
cathode such as found
in 5AR4. The cathode is a tube with special oxide coating, and
inside the tube there is a
heating element also called a filament, or just heater, and is a
folded or coiled wire also
coated with an oxide to stop direct contact with cathode. This
allows the cathode to be
heated by an independent heating supply of Vac.
(A) shows the electron flow with anode positive, and (B) shows
electrons not flowing if
anode is negative.
(C) shows the schematic in a circuit where electrons flow around
the circuit.
To understand relative electrical charges, always consider a
circuit as shown in (C)
where there is a 0V rail which is at the same voltage potential,
or charge potential as
MOTHER EARTH. In practical terms, it means that the black lead of
a voltmeter is
always connected to 0V rail and the red lead used to measure DC
Volts or AC Volts
with static or changing levels of positive or negative Volts above
of below the
REFERENCE level of 0V.
In Fig1, (C) shows a heater filament powered by 5V at 3A, and
could be ac or dc current,
and this current flows around the circuit formed by 5Vac supply,
filament, and part of the
0V rail. The 0V rail is assumed to have such low resistance that
any current flow does
not cause a significant Vac or Vdc across the portion of 0V rail
in circuit.
In Fig1, (C) shows a 250Vdc supply with +250V connected to a diode
anode via 2k0
resistor, and cathode of diode connects to 0V along with negative
side of 250Vdc supply.
Dc flows around this circuit. Conventional current flow has been
assumed to be positive
to negative for centuries, but after the discovery of electrons is
from something negative
to something positive. Some say the current is a flow of holes in
something positive where
the holes are vacancies in electron orbits around an atom which
lack an electron.
The absence of electrons makes something more positive, and the
surplus of electrons
can make something negative.
Some electrons are pulled away from space charge around cathode
because force of
attraction produced by positive anode is greater than any force
acting to return the
electrons to cathode. Electrons drawn away from cathode begin
filling up holes in
anode and the anode Vdc falls according to Ohm's Law E = I x R. if
100mA flows in 2k0,
the Vdc across 2k0 = 200Vdc, and because the VDC supply is kept
constant,
Ea = +250Vdc - 200Vdc = +50Vdc.
These conditions can only remain constant where the cathode can
draw more
electrons to replenish those lost from space charge. This easily
occurs from the
negative supply side of PSU which connects to 0V rail. The steady
flow continues while
the PSU is connected. If we assume the PSU has zero resistance,
then power dissipated
as heat in 2k0 RL = 200V x 0.1Adc = 20W, and in diode, 50V x 0.1A
= 5W, so the PSU
must provide a total of 25W of power to diode and RL.
In the real world, the PSU may be a transformer winding producing
mains Vac, and
power is only produced in RL when Vac waves rise above 0V, because
current cannot
flow when anode is below 0V, ie negative, for 1/2 a sine wave
cycle.
I make no apologies for the greater men who made past discoveries
and who
were forced to consider the opposite action was going on to what
was first analysed.
Later discoveries yielded "more truth" about everything.
Current flow needs far more explanation than I offer here, but we
can just accept
the conventional idea that anode current is from anode to cathode,
while knowing
electrons flow the other way.
This contradictory convention should never stop anyone
understanding all basic
electronics with vacuum tubes and networks with R, L and C, and
building fabulous
amplifiers.
The glass bulb "valve" later evolved to a glass cylinder tube
sealed at each end and
with connection pins or metal caps at each end or at one end only.
In the USA, valves
were commonly called tubes.
The flow of electrons between cathode and anode require these
electrodes operate
in a "hard vacuum" with extremely low amount of gas
molecules present.
To ensure the vacuum remains pure, a coating of metallic barium is
sprayed onto inside of
glass bulb, and hence you see silverish patches at top of tube or
bottom.
These attract gas molecules which combine with barium and are
there are few free gas
molecules inside tubes working properly. Such molecules can become
positive gas ions
stripped of an electron, and they bombard the cathode with such
kinetic energy they slowly
erode the cathode coating causing lower electron emission.
Here is a picture of a typical rectifier diode Ra curve -
Fig 2. Vacuum diode Ra curve.
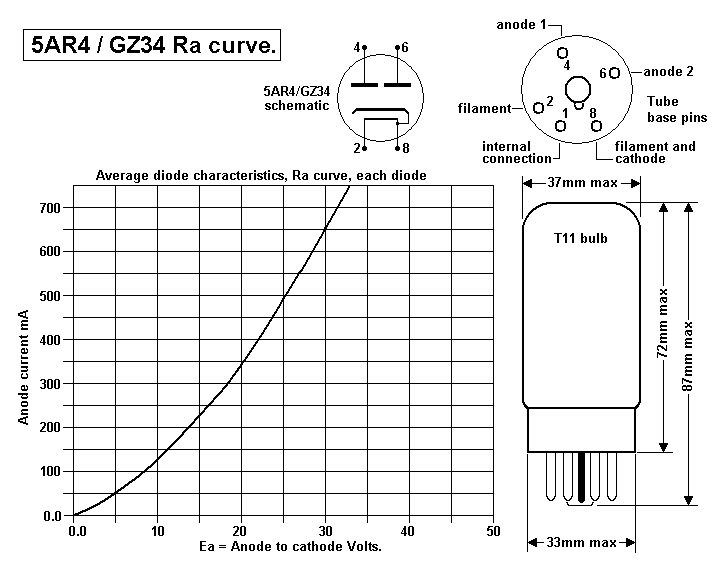
Fig 2 shows the Ra curve for diode of two inside a GZ34 aka 5AR4.
The curve is drawn by raising Ea above 0V and measuring Ia flow.
At any point
along the curve, a tangent may be drawn which is a straight line
and the Ea change
and Ia change measured for 2 points on that line.
The dynamic anode resistance = Ra = E / I = change of Ea / Change
of Ia.
The Ra is higher ohms at low Ia. At Ea 10V and Ea 125mA, Ra
changes according to a
resistance equal to a tangent line to the curve at 10V x 125mA. a
large change of Ea,
say +/- 5V will give non linear Ia change because Ra varies around
a value of 60r at
10V x 125mA, according to above curve. An average Ra is quoted for
5AR4 anode
resistance of about 30r for each diode, and this is fairly low
compared to most other
vacuum tube rectifiers.
The Ra curve does not tell you there are strict limits on maximum
anode cathode to anode
current in diodes and in most tubes generally. If the peak Ia
exceeds the limits, the there
can be arcing between anode and cathode which can damage the tube.
------------------------------------------------------------------------------------------------------------------
THE TRIODE. The vacuum triode has similar anode and cathode
to to a diode but has a
single grid electrode placed between the two. The grid is usually
a coil of fine wire wound
around two support rods to which the fine wire is spot welded.
It is concentrically aligned with anode and cathode, and grid
wires are close to cathode,
within 1mm, but with larger distance from anode.
Anodes are often made with two half tubes with flanges each side
which a press fitted
together so that the flanges can help radiate heat away.
The electrodes are held in alignment by mica sheets at top and
bottom of the
assembly to keep them positioned and well insulated from each
other for up to 40,000
hours at high temperatures where use of plastics is impossible.
There are 2 different
types of glass for bulb and the base.
Copper wire leads are spot welded to rods supporting cathode,
grids, or anode,
and penetrate the glass base to then connect to pins in an octal
tube base, or the wires
connect to pins held firm in glass base. The sealing of wires or
pins in glass is done
by melting the glass around the wires or pins to form an very air
tight seal.
Most of the fine delicate work of manufacturing vacuum tubes has
always been
done by skilled teams of women naturally good at sitting for long
hours doing craft
work viewed though a magnifying glass. As tubes became
miniaturized, the men and
women in factories suffered eye strain. There were limits to how
small a vacuum tube
could be made, and eventually, someone developed transistors which
could be made
so small there are millions of them in a mobile phone.
Inside the glass bulb there are silver coloured sprays of barium
metal which are placed
during RF heating of the tube when all air and gas has been
extracted. This metal is called
the getter, and it will absorb minute amounts of oxygen and
nitrogen or carbon dioxide
molecules to form metal oxide, thus keeping a pure vacuum
environment for the life of the
tube. Tubes are allergic to presence of any gas molecules and
despite best efforts by
manufacturers, there are minute amounts of air left inside
the tube or which are trapped
inside the metal which later are exuded over time. As a tube ages,
the silver gettering
becomes discoloured by oxide formation which may indicate
remaining tube life is short.
If the glass is broken, air rushes in and gettering turns to a
white powder, and the tube
cannot ever work again.
Fig 3. Triode internals.
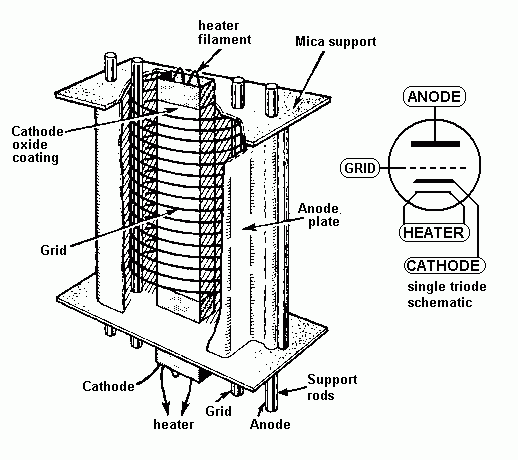
Fig 3 shows construction details of a typical indirectly heated
triode.
There are images online for directly heated triodes such as 300B,
845. DH triodes of
300B size or less operate at red temperature, or less than 900C.
They are optimal for
Ea up to +900V, as are indirectly heated cathodes but above 900V
the tungsten cathode
wire doped with thorium is the most rugged cathode which will work
fine at white heat
at 2,000C+ like an incandescent lamp globe. Thus B+ for such tubes
as 845, 211, 213
can be 2,500Vdc. There are tubes so big they are made of steel and
a man can walk
inside through an access door to replace DH cathodes rated for
hundreds of amps.
See online images to satisfy your curiosity, but don't try to buy
a pair of biggies for hi-fi
because they will cause an instant divorce, and even your dog will
leave.
Directly heated tubes such as 300B tend to be much more
microphonic than indirectly
heated tubes. Audio vibrations of DH tubes cause minute movement
of their more more
flexible cathode and grid structures. The metal electrode parts
become resonant to
give a metallic ringing sound from speaker if tube is pinged with
a pencil. The vibrations
cause minute change of distance between cathode and grid thus
modulating electron
flow, often at one or more frequencies. the 300B was the tube GE
developed for audio
amps for movie sound in amps they leased to theater owners.
The projector room
with its amps were fairly quiet, so noise did not cause noise the
audience could hear
from large horn loaded speakers. Similarly in a typical
lounge-room, the audio sound
level has to become deafening before the 300B is affected.
So under normal use such microphony is rarely a problem in output
triodes but can
be a problem for any input tubes including indirectly heated
triodes or pentodes etc.
Old tubes may develop loss of grip by mica sheets allowing
electrodes to rattle slightly,
and perhaps become so bad you hear a squeal of acoustic feedback
even at low levels.
Input tubes for microphones or phono stages MUST be chosen for low
noise and low
microphony.
Noise in triodes is generally lower than pentodes or other tube
types, and a good
sample of 6SN7 or 6CG7 will have input noise of 1uV. Many will
measure 3uV even
when new. The noise varies in spectral profile, with most at low
F, like a rumbling
waterfall when amplified 2,000 times. RDH4 talks at great length
about noise generation
in vacuum tubes, and explains "shot noise", and other causes of
noise. Old tubes
develop sputtery noise with LF bursts and if noise > 3uV, they
should not be used
for an input tube or in a preamp tube. Often you will find a "NOS"
6SN7 is not as new
as the seller says, and may have had 10,000 hours of use, but
noise = 8uV, lots of LF
rumble, and you find the grid Vdc to 0V is a positive +1Vdc or
more across a bias Rg =
220k, when a healthy tube might have a slightly negative Vdc
across Rg. Some may
have discoloured getters, and those which are noisy, microphonic
and with spent getters
are useless and must be sent to hazardous waste recycling /
disposal.
There are three parameters of a tube which are important for
design purposes :-
Ra, anode resistance is the dynamic output resistance which can be
measured
when connecting anything to the to the anode.
Ra is NOT calculated by measuring Ea between anode and cathode in
a working tube
and the Ia flowing, and calculating Ra = Ea / Ia. It is wrong. The
calculation of Ea / Ia
is valuable for calculations of RLa, the anode load for any tube,
but not for calculation of
the dynamic anode resistance Ra.
Ra is calculated by measuring a small change of Ea and Ia and then
calculating
Ra = Ea change / Ia change.
This is done by setting up a triode with wanted Ea and Idc and and
with grid at 0Vac,
but biased with -Vdc for the wanted Idc.
The Idc to anode MUST be from a Z source at least 30 times the
suspected Ra of the tube.
With say 6550 in triode mode, Ra will be between 900r to 2k2, so
the Idc feed from B+
could be a choke with Z = 60k to allow Vac test signals at 1kHz.
Thus a choke with XL = 60k at 1khz will be 10H, and maybe too hard
to buy cheaply if
rated for say 100mAdc. The other Best Thing is a CCS made with
solid state with HV
rated BJTs. These can have Z at 1kHz of over 1M0, and the CCS
finite R will not make
any difference to the Ra measurement.
To measure Ra :- A 4.7uF MKP type, 1,000V rated is connected to
anode which could
have +450Vdc. Output end of cap then connected to say 1k0 5W which
connects to a low
Z Vac source of a signal generator or audio amp. 10Vac at 1kHz
source is plenty to make
the measurement. The Va, ie, Vac between anode and 0Vis measured
and recorded.
The Vac across the series resistance is recorded.
Ra is calculated = Va / ( Vac across R / R ).
For example, for a 6550 connected as a triode, Ea = +450Vdc, Iadc
= 50mAdc, and use
1k0 current sensing R. The 4u7 has Xc = 34r at 1kHz and makes no
difference to
measurements. Suppose we measure Va = 5.5Vrms, and Vac across 1k0
= 5.0Vrms,
then Iac in 1k0 = 0.005A, and
Ra = 5.5V / 0.005A = 1,100r, or about 1k1.
If the 6550 triode under test has cathode bias with Ek = +58V and
grid at 0V, with anode
at +508Vdc, then Rk would be 58V / 0.05A = 1k2. This MUST be
bypassed with at least
100uF, but could be 470uF. The added unbypassed Rk will make Ra
measurement
completely wrong and you might measure "Ra with unbypassed Rk"
which may have a
value here at 9k3.
The highest Ra for triodes might be for 1/2 12AX7 with Ra = 65k,
and always with
bypassed cathode. For tests of high Ra above say 5k0, the choke
must have more
inductance so more than one would be needed so that the CCS
becomes the better hi Z
dc feed for Idc.
The alternative method to calculate Ra requires more education,
and can be more
reliable than always using a CCS feed as mentioned above. Two gain
equations are used
for for two different RLa loads while keeping the Ea and Idc and
grid input Vac constant,
and with cathode well bypassed, and with all Va having THD <
2%.
For all tubes, Gain = Va / Vg = µ x RL / ( Ra + RL ). This is the
most suitable for triodes
with µ < 100 with expected Ra < 100k.
To understand how to measure & calculate the Ra, µ and gm for
large number of small
signal triodes, pentodes, triode-pentodes, hexodes etc, you will
need a test circuit similar
to what I made to accurately observe tubes I wished to use.
Fig 4A. Schematic for measuring Ra, µ, gm of small tubes,
12AU7, etc.
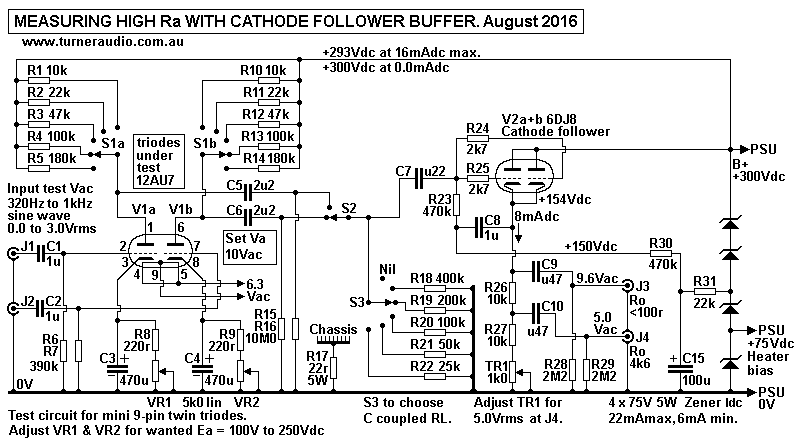
Fig 4 allows measurement of Ra, µ, gm and noise generation of any
small signal triode.
Tubes to be tested are plugged into mini 9 pin socket on left
side, under S1a and S1b.
S1a+b select the dc feed RL to each V1 anode.
Wanted idle Ea and Iadc is adjusted by VR1 and VR2.
Input Vac is applied to V1a or V1b grids at J1 or J2.
For gain measurement with chosen RLa from
S1a or S1b, Vac input is adjustest to get 9.6Vrms at output of V2
cathode follower.
S2 selects anode output Vac from V1a or V1b for input to V2a+b
grids.
S3 selects C coupled anode load for V1a or V1b, so that C coupled
load for V1 anodes may be changed
without change to Idle Ea and Idc conditions.
V2a+b is paralleled 6DJ8 cathode follower which allows measurement
of Vac from anodes of tubes
tested without test probles or meter input resistance affecting
Vac at anodes.
Tubes for testing can be mini nine pin twin triodes such as 12AX7,
12AY7, 12AU7, 12AT7, 12BH7,
6DJ8, 6CG7, all non-power tubes. For mini 9 pin ot 7 pin pentodes
or octal tubes, additional sockets
and switches must be used.
The "12" in 12AX7 etc means heater Vac or Vdc can be 12.6V,
applied across pins 4 to 5, and pin 9
is the center join of 2 heater filaments. But 6.3V may be applied
between 4+5 connected together
and pin 9. I show R31 + R32 100r providing resistance center tap
for 6.3Vac, and all heaters are
biased at +75Vdc from Zener diode string.
The "6" in say 6CG7 triodes is for 6.3V only, with both heaters in
parallel and between pins 4 and pin 5.
Pin 9 is a screen between each triode anode and is usually taken
to 0V, but may be left unused for where
the two triodes are paralleled.
V2a+b 6DJ8 cathode follower has overall gain = 0.96. For 10.0Vrms
at V1 anodes, Vac at J3 = 9.6Vrms.
J3 has Rout < 100r, and Vac meter input resistance or
capacitance will not cause any errors.
J4 gives Rout = 5k2 approx where TR1 is adjusted to get J4 Vo =
5.00Vrms with 9.6Vrms at J3.
Thus is is easy to calculate the real Vac at V1 anodes by
measuring Vo at J4 and multiply x 2.0.
Once TRI has been se to get 0.500 x V1 anode Va, the setting will
not need to be changed for years.
The S1a + S1b can be two pole 6 position wafer switch. These
switches will easily carry the Idc to each
anode of V1, and allow variation of RLa between 10k0 to 180k. S2
is 1 pole 6 position rotary switch.
Output from V1 anodes is via C5 and C6 2u2 to S2 which selects
which anode signal Va is to be fed to
V2a+b grids. R15+R16 10M0 keep S2 output at 0Vdc, and have
negligible loading effect. If the highest
RLa = 180k, with 6M8 in parallel, RLa = 175k, a change < 2%,
which will not change calculations for
Ra, µ more than 1%.
Input resistance to V2 grids has R23 470k bootstrapped from V2
cathodes so its effective R = 13M effectively
so that additional total loading apart from S1 or S3 resistors =
10M0 // 13M0 = 5M6.
To calculate total load for gain measurements with S1 set for
180k, S3 set for 400k, total RLa =
180k // 400k // 5M6 = 121k.
With 12AU7, and for Ea = 110Vdc, Iadc in 180k = 190Vdc / 180k =
1.056mA and Ek will be +5.5Vdc approx.
Total Rk may be 5k2, so VR1 or VR2 may be adjusted for nearly
maximum at just under 5k0. For where dc RL
is lower value, and Idc higher, the VR1+2 should give enough Ek
variation for a wide range of triode type numbers.
Consider test of V1a = 1/2 12AU7 with dc RL set at 47k, and
Ea set at +150Vdc. With B+ = +297Vdc,
Iadc = 147V / 47k = 3.13mAdc, and Ek may adjusted by VR1 to be
about 6.0Vdc. Ea = 144Vdc.
1. Connect a signal gene to J1 input and apply 400Hz sine wave so
that 9.6Vac appears at J3.
Adjust TR1 so that 5.0Vac is measured at J4. There should be
10.0Vrms at V1a anode.
2. Use S3 with Nil C coupled RL.
3. You may find input Vac at J1 = 0.765Vrms.
Gain = Va / Vg1 = 10.0V / 0.765V = 13.07. Call this gain = A1. RLa
= 47k // 5M6 = 46.6k = RL1.
4. With no change to Vin, set S3 for C coupled load = 100k.
Measure Vac at J4, and suppose this is 4.51Vac, so Vac at anode =
9.03Vrms.
Calculate gain = 9.03V / 0.7659V = 11.805, call this gain
A2. RLa = 46.6k // 100k = 31.8k = RL2.
5. For all tubes gain A = µ x RL / ( RL + Ra ). Therefore µ = A x
( RL + Ra ) / RL = A x [ 1+ ( Ra / RL ) ].
The µ and Ra for both loads RL1 and RL2 is the same, with RL and
Gain A1 and A2 different.
Therefore µ = A1 x [ RL1 + Ra ] / RL1 = A2 x [ RL2 + Ra ] / RL2.
Thus A1 x [ 1 + ( Ra / RL1 ) ] = A2 x [ 1 + ( Ra / RL2 ) ]
Thus Ra = [ A1 - A2 ] / [ ( A2 / RL2 ) = ( A1 / RL1 ) ]
= [ 13.07 - 11.80 ] / [ ( 11.8 / 31.8k ) - ( 13.07 / 46.6k ) ] =
1.27 / 0.091k = 13.95k
6. For RL1 gain, substitute Ra 13.95k, µ = 13.07 x [ 1 + ( 13.95k
/ 46.6k ) ] = 16.98.
7. V1a Gm = µ / Ra = 16.98 / 13.95k = 1.217mA/V.
8. There is an easier way to find Ra !!!
Ra - Va change / Ia change for the 2 RLa values, while input Vac
remains constant.
10Vrms / 46.6k = 0.2146mA, 9.03Vrms / 31.8k = 0.284mA.
Ra = 0.97V change / 0.0694mA change = 13.98k.
µ = 13.07 x [ 1 + ( 13.98k / 46.6k ) ] = 16.99.
Gm = 16.99 / 13.98 = 1.215mA/V.
Ra is the triode "internal dynamic resistance" which is
result of anode Vac change producing Ia change
because anode has gm. The above test of 1/2 12AU7 had 10Vrms
between anode and cathode, and Ra is like a
resistance between anode and cathode, and was found to be 13.98k,
so Iac flow in Ra = 10V / 13.98k = 0.715mArms.
The load current = 10V / 46.6k = 0.2146mA, and the grid Vac must
produce a total Ia change = sum of Ra and load
currents = 0.9296mA, and Vg needed = total Ia change / gm =
0.765Vrms.
If Ra is known anode gm = 1 / Ra = 1 / 13.98k = 0.0715mA/V, and
while this is a small percentage of g1 gm the
effect of anode gm is that of applied local NFB which reduces Ra
and THD which would both be much higher values
if the 12AU7 was replaced by say 6BX6 pentode with the same idel
Ea and Iadc.
These results confirm most data sheets for 12AU7 are about
correct.
Results are same for both methods, but if the load values and Vac
are not measured within +/- 5%,
it is very easy to get errors fort Ra, µ and gm which are +/ -
50%, or what seem to be nonsense.
Transconductance, gm, is measured in mA / V and is the
ability of the grid to change anode current.
It could be be easily measured with the anode at a fixed B+ and
with small resistance between B+ and
anode = 100r. The idle current is set for the Iadc wanted.
Vac is applied to g1 grid, but this must not exceed 1/2 the bias
Vdc, so for above 1/2 12AU7, Vpk
must not exceed 3Vpk, say 2.12vrms. This keeps Vpk input from
causing high THD in anode current changes.
For the 1/2 12AU7, expect Iac = 2.57mArms which will appear at
100r anode load = 0.257Vrms.
The 100r load is so much smaller than Ra that there is no need to
calculate gain with Ra included.
Thus 2.12Vrms causes 2.576mA Iac flow, so gm = 2.576mArms /
2.12Vrms = 1.215mA/V.
This simpler method of measuring triode gm is only valid for where
negligible Va change occurs.
For all triodes, pentodes, beam tetrodes and frequency converters
etc, the gm can change very
much for large changes of Iadc. Generally, the µ is the most
constant parameter, ie, the product
of gm x Ra, so where Iadc is low, gm is low, Ra will be high, and
for high Idc, gm is high, Ra is low,
compared to a middle value.
Gm and Ra change during each wave cycle and it is these changes
that cause the distortion which
may be typically 1% for Va = 10Vrms for 1/2 a 12AU7 above. The THD
will be mainly 2H, and affects
measurements and calculations of parameters.
Amplification factor, µ, is just a number = gm x Ra without
units and is the voltage gain of a triode
or other tube when NO load with infinite ac resistance is
connected.
µ and gm and Ra are related to dimensions between cathode and grid
and cathode and anode, and
is is beyond my duty of care to have 5 more screenfuls of
information here about how distances between
electrodes affect the main 3 parameters.
But the closer grid is to cathode, the higher the gm. The closer
anode is to cathode, the lower the Ra.
There are limits to how close electrodes can be and determined by
safe practices during manufacture
to avoid internal arcing.
Fig 4B. PSU for schematic in Fig 4A.
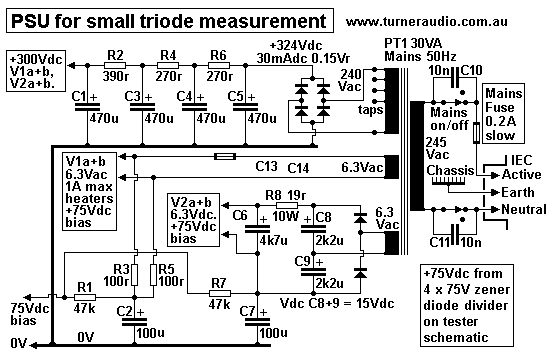
Fig 4B is a generic PSU with tapped HT winding to adjust B+. In
Fig 4A, I show +300Vdc rail shunt regulated
with 4 x 75V zener diodes. Max Idc in Zeners = 22mAdc, so each has
max Pd = 1.65W, which is a little high.
But use of 6 x 50V would better if other changes to circuit are
made. Without any regulation, expect LF B+
rail changes of +/- 50mVpk. The CRCRCRC filter has pole at about
0.3Hz, which means B+ rail could slowly
increase or decrease +/-50mV or a lot more. Some kind of active
regulation will work better but slow changes
of B+rail will not affect measuring Ra, µ, gm, and meters or CRO
with pole at 10Hz should keep B+ change
to negligible levels.
The heater supply to V2 6DJ8 is Idc, to reduce hum at J3, J4.
Heater of V1 tube under test is Vac, and if there is leakage
current from cathode to heater the hum at V1 anodes
can be much more than the grid input noise which is less than 1uV
for a good tube sample.
With Idc heating, the leakage k-H may not be noticed.
For measuring input noise of the tubes, the output of J3
may be fed to low noise amp with gain of say 2,000
over 10Hz to 20kHz bandwidth. The J1 and J2 have shorting plugs
used to ground the grids to 0V.
If 1/2 12AU7 has input noise = 1uV, and its load gives gain of
13.0, then at least 13uV of noise is at anode.
When amplified x 1,000, there is 26mV noise at amp output which
may be very clearly heard using a quiet
power amp and a speaker. Noise will be mix of 50Hz hum, plus sound
of gushing water, plus pops and snaps
and sizzles of a BBQ. Bad tubes have input noise > 3uV, and a
small tap of tube with pencil will reveal any
microphony.
The methods above for measuring Va with 2 different load values is
best for calculating Ra.
The use of a small anode resistance is easiest for measuring gm.
Then it is easy to calculate µ = gm x Ra.
For a pentode, Ra may be 500k, and gm = 2mA / V, so µ = 1,000.
Fig 5.
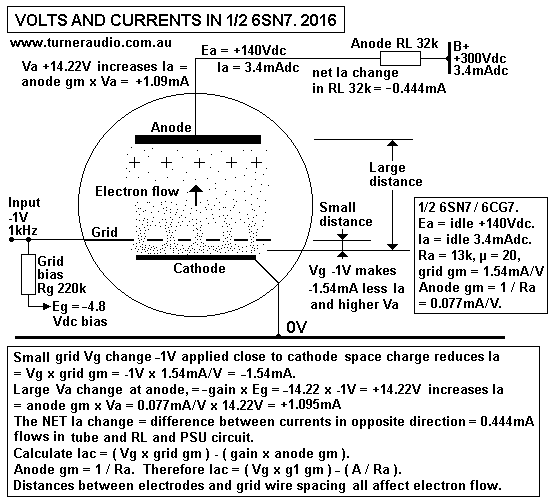
Fig 5 shows a 1/2 6SN7 The distance between cathode and control
grid is much smaller than
distance between between cathode and anode. This means a small
Vg-k signal has a large effect
on Ia flow, and the effect of larger Va-k signal has a lesser but
very significant effect on Ia flow.
These relative distances have a large effect on the Ra and gm, and
hence on their product = µ.
The spacing of grid wires wound around support rods also affects
the characteristics.
I don't have space or time here to give a grandiose lecture on how
to make a triode including all the
formulas which have been used for decades. But as you can see, the
space charge electrons in
cloud around the cathode are subject to the electrostatic field
effect of nearby grid wires and more
distant anode.
The electrostatic field is created by voltage potentials of the
electrodes, and the field strength or
intensity is inversely proportional to distance squared. This
means that the force acting on an
electron due to a field is quartered if the distance is doubled,
or that force is quadrupled if distance
is halved. It is a non linear transfer function. The electric
field resembles light intensity which follows
the same rule.
Midway between grid wires the grid field is low, and the field
effect of the distant anode can be felt by
some of the electrons between grid and cathode, so these are
attracted to make the journey to anode
after slipping past the gaps in grid wires which are negative. The
negative grid speeds up those
electrons once they get past the grid, and they continue to anode
at an amazingly high speed to
anode where they are absorbed into available orbits around the
metal atoms.
The available orbits lack an outer electron, ie, the atoms have a
hole, to be filled with the incoming
electron.The holes are what makes something more positive. Not all
electrons have an easy landing
and some bounce away from anode but then make a second landing
attempt, its called "anode
secondary emission" The absorption of electrons into anode causes
anode heating = ( Ea x Ia ) Watts,
and for 140Vdc x 3.4mA in Fig 4, Pda = 0.476W, which hardly warms
the anode more than it is already
being heated by radiant heat from the cathode where its filament
heater makes Pdk = 6.3V x 0.3A = 1.9W.
Usually a 6SN7 can be touched without getting a burn when turned
on.
The two fields produced by grid and anode have joint control of
the electron flow. The space charge
electrons "feel" the force effect of the anode voltage field
because there is open space between grid
wires; if the grid was a sheet of metal the anode field would be
interrupted completely. Some reduction
of the strength of field effect by anode is due to the grid's
field around each grid wire, but the two
electrodes of grid and anode still have a summed effect on the
space charge. If the grid becomes
negative enough, its negative field is high enough to prevent all
the effect of anode to be obscured,
and no Ia flows an the triode current is cut off. With grid V
becoming close to cathode V or perhaps
positive, the grid can allow maximum Ia flow to anode, usually
well above what is used for class A
operation.
I show -1V applied to the grid from a low impedance signal gene.
The grid produces inverted anode
output = +14.22Vrms. This has effect of increasing Ia by V change
/ Ra, or in effect, by V change x
anode gm and anode gm = 1 / Ra. The gm effect is inverting, ie,
the anode acts as if it is a grid with
gm of 0.077mA/V and with positive going Va, there is less current
in RL but more in the tube.
However, the - grid Vg cause less Ia and a current change opposite
to the increase caused by Ea going
positive, so the NET current in tube is the sum of the gm effects
by anode and grid, and thus the current
change in RL is the same as for for the tube, which we know MUST
be the same, because the tube
plus RL plus PSU make the necessary circuit for the flow of
current. There can be no continuous current
flow without a circuit.
While the grid remains negative there is no current flow into or
out of the grid and the grid is an extremely
high impedance input terminal. At a very low Eg, say -25V, there
is no Ia because the -25V overwhelms
any effect the anode Ea might have unless Ea was extremely high
which may lead to arcing.
There are limits for maximum Ea to enable linear operation within
Pda ratings. But as Eg rises from very
low, Ia begins and gm varies considerably in proportion to a non
linear formula, gm = K x square root Eg cubed.
This gives the classic Ra curve shape for triodes and for diodes
where anode voltage controls Ia flow entirely.
This equation is not exactly correct because of shaping of
electrodes and grids, but it is approximate.
In the middle region of grid control, the current change is
acceptably linear for triodes.
The anode load value for triodes has a huge effect on linearity,
with most distortion produced where RLa < Ra,
ie, a load line on loadline graph approaches vertical. Least
distortion is produced with RLa many times Ra,
ie, the loadline approaches horizontal. So for small signal
triodes, RLa should be always > 4 x Ra for good
linearity. Best linearity is where RLa = CCS, or > 10 x Ra.
The grid needs no input power to control Ia while its Eg remains
negative. All tubes which swing positive
will draw current for the positive part or all of the wave cycle
and thus become a low input resistance which
require a low output impedance driver such as a direct coupled
cathode follower, or a transformer winding
powered by a small power tube.
Where the grid is driven positive above Ek, most electrons flow
past the positive grid to the more positive
anode but those which are absorbed by grid cause it to heat up,
and there is a strict limit on the temperature
rise and grid dissipation Watts. Usually this is only ever
something to worry about in class AB2 operation of
power tubes, and is of no concern in signal tubes.
In small signal amps and most power amps the grids are never
driven positive and all current control is done
with by Eg change between 0V and some -Eg which produces Ia
cut-off.
Fig 6.
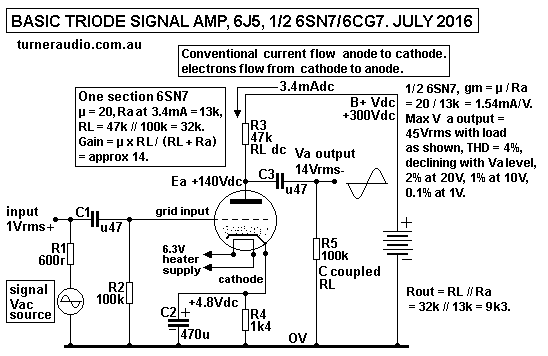
People with a keen eye for detail and a mind full of common sense
will see that electrons are emitted from
the cathode and travel upwards past the grid to the anode. Yet
they see the 3.4mA of anode current flow
indicated as a flow downwards by the arrow and through R3 RLdc
47k, to anode, through vacuum
to cathode, through R4 1k4, and on through 0V rail to negative
side of grounded B+ supply.
The triode allows conventional direction of current flow shown,
but in fact electrons flow the other way,
and the rules and formulas remain valid for most ppl who consider
such simple circuit operations.
I will not rock the boat to change the conventions. We don't
really need to be mindful of the trillions
of electrons flowing each second from cathode to anode, let alone
give each one a name. We need
to be able to have a mental picture in the conventional sense and
about the electron activity sense.
After a short time delving into basic electronics we realize quite
a few things don't seem to comply
with commons sense notions. ( For example, a resistance with lots
of ohms is an easier load for a
amplifier to power than a low number of ohms.)
For Vdc input signals, 470uF is an open circuit and R4 1k4 gives
local current NFB which lowers
gain to 14.22 / ( 1 + [ 14.2 x 1.4k / 32k ] ) = 8.77, so gain at
Vdc is -5dB. This is of little interest
because we want wide AF bandwidth with little bass attenuation so
C2 bypass cap should have a large
value to give a flat response and little added phase shift to well
under 10Hz. For Vac, C2 bypasses the
1k4 plus parallel resistance looking into cathode which is
approximately RL / Gain = 32k / 14.22 = 2k2.
The total R to be bypassed = 858r. Xc should be < total R at
1Hz, which requires 185uF for this case.
220uF or more is adequate for almost for good Vac bypassing.
In the schematic, the "indirectly heated" cathode is heated by Vac
supply which has no connection or
effect upon the triode operation for signal Vac. Some cathodes are
"directly heated" with their special
metal designed so they can be heated by Vac or Iac and the Vac or
Vdc heating supply is connected to
cathode and signal path but is done in such a manner to not
interfere with signal Vac.
DC operation of the triode in Fig 6.
Fig 6 schematic is a very basic triode amplifier using one triode
of a pair inside a 6SN7 twin triode.
The 3.4mAdc generates +4.8Vdc in R4 1.4k, ie, Ek = 4.8Vdc. The
grid bias Vdc is same as 0V rail because
of biasing R2 100k from 0V rail to grid. Therefore the grid is
-4.8Vdc below the cathode Ek, and Eg1 = - 4.8Vdc.
The cathode Ek is what is also known as the quiescent cathode bias
Vdc which makes the grid negative
in respect to the cathode. If Ia increased, Ek would increase,
thus increasing Eg so the Ia is reduced by
any tendency for Ia to increase. This is a local current NFB
effect. It does not occur with audio frequency
signals because R4 is bypassed with C2 470uF. The amount of local
current NFB is not high, but enough
to keep Ia better regulated than if cathode connected to 0V and a
fixed grid bias of -4.8Vdc was applied
to bottom of R2 100k.
Fig 6 shows very common class A operation for a 1/2 6SN7 used in
countless small signal amps since 6SN7
was developed in 1930s. Tube data sheets with "Ea vs Ia
characteristics" will show triode Ra curves for
values of Eg bias and the shape of curves are similar to Fig 2
diode above.
The chosen idle working point in Fig 4 is Ea 140Vac, Ia 3.4mAdc,
with B+ at +300Vdc. The anode load is
the R3 47k dc carrying RL and the cap coupled R5 100k RL which has
no Idc flow. The total anode
load = R3 // R5 = 47k // 100k = 32k. Voltage gain = µ x RL / ( RL
+ Ra ) = 20 x 32k / ( 32k + 13k ) =
14.2, approx, so expect Gain A = 14.0.
This means if 1.0Vrms+ is applied to grid, there will 14Vrms- at
anode.
The + and - signs indicate phase of signals and that the output
wave is 180 degrees to input, ie, the shape
of input wave is the same as output, but output is upside down. In
other words, the grid is "an inverting input"
because it produces an inverted output.
Load line analysis using "Ea vs Ia characteristics" on data sheets
will show what possible good working points
are for good linearity and wide dynamic range for any tube. I
started with B+ of +300V, then chose R3 RLdc
= 47k, and plotted where Ia = 3.4mA 47k load line, and this point
was at Ea = 140Vdc, and it is the Q point
for quiescent dc operation. Inspection of nearby Ra curves for
various -Eg1 values would show Eg1 at Q
= about -4.8V, and that a tangent line to Ra curves at Q would
show Ra = approximately 13k.
The Q point for dc allows Vac operation with peak swing of +/-
62Vpk, or 44Vrms for the total anode load of 32k.
For dc operation, the R4 cathode resistance needs to be chosen
carefully to ensure cathode bias Rk gives
the correct grid bias to have Q settle where we wanted it. With no
Rk, Ea would be far too low, and if Rk
was too high, Ea would be too high and only a narrow range of Rk
values gives Ea within a good working
point area.
After choice for Ea and Ia, Rk can be calculated :-
Rk = [ wanted Ea - ( Ia x Ra ) ] / ( µ x Ia )
= [ ( 140V - ( 0.0034 x 13,000 ) ] / ( 20 X 0.0034 ) = ( 140V -
44.2V ) / 0.068 = 1,408r.
Put more basically, Consider Ia = 3.4mAdc, and Ra curve for for
Eg1 = 0V. Between 0.0mA and 3.4mA, the
slope of Ra curve is roughly equal to a straight line = Ra = 13k,
so for 3.4mA on this Ra curve,
Ea = Ia x Ra = 3.4 x 23k = +44.2V.
The idle condition has Ea = +140V at 3.4mA. The difference of Ea
between the 2 points = 140V - 44.2V = 95.8V.
To achieve this difference in Ea with Ia constant at 3.4mA, the
change of Eg = Ea change / µ = 95.8 / 20 = 4.79Vdc.
The cathode Ek must be 4.79V above grid Eg at 0V bias, so a
cathode Rk can be
calculated Ek / Ia = 4.79V / 3.4mA = 1k4.
Having said all this, few will understand, but after some study
and some experiments with a triode on a bread
board or old chassis then understanding gradually occurs.
Do not just simulate with a PC program. That is how you
will stay ignorant and lazy. You need to work
everything out using applied principles and a pocket calculator.
Once that is achieved, a simulation program
can be used to confirm your measurements or calculations.
For Fig 6, and with Rk = 1k4, the effective Ra at dc condition is
calculated :-
Ra' with unbypassed Rk = [ ( µ + 1 ) x Rk ] + Ra = [ 21 x
1k4 ] + 13k = 42k4.
If R3 RLdc is 47k, and B+ is raised to +350Vdc, then you have R
divider with 47k + 42k4 in series = 89k4.
The Vdc change = 350V = 300V = +50V, so Ia change = 50V / 89k4 =
0.56mAdc, so Ia increases from 3.4mAdc
to 3.96mAdc, and the Vdc across 47k = 186.1V so it B+ = +350V,
then Ea = +163.9Vdc. The Ek will also
rise from 4.8Vdc to +5.54Vdc. Such a change of B+ will make almost
no difference to the signal operation,
but max Va will be higher. If B+ was lowered to +250V, the Ia
would be less, and max Va less, but little change
would occur for signals. But the higher Ea permits a higher RLdc
value with same Ea kept at +140Vdc.
With a higher total anode load for triode, there is less THD. In
other pages at this website I have used a
CCS to supply Idc to input tubes which raises RL so much the THD
is 1/3 of what it is in Fig 4.
----------------------------------------------------------------------------------------------------------
Model of vacuum tube as an equivalent Voltage Generator.
The model of a tube as Voltage Generator plus series Ra involves
the use of our
imagination to better understand the function of tubes and to
analyse circuit performance.
Fig 7. Vac generator model of 6SN7.
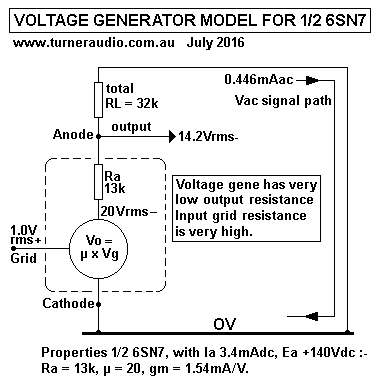
Fig 7 has the basic triode model for 1/2 6SN7 in Fig 6, contained
within dashed line. All Vdc and Idc
arrangements are ignored, and only the Iac operation is considered
for the known data parameters
Ra, gm and µ for a pre-known dc operating condition listed in Fig
6.
Every tube can be modelled as a very low impedance voltage
generator whose output across two terminals
is the product of µ x Vg where Vg is an applied Vac between a high
Z input third terminal and one of the
other two terminals. In this case, the bottom gene terminal is the
cathode, the input is the grid, and the top
terminal is the imaginary generator output and anode is the top of
Ra in series.
Fig 7 shows the model for a 6SN7 as a low resistance Vac generator
producing 20Vrms output for 1Vrms
grid input voltage. The Ra of 13k is not a real resistance, but
the effect of Va on Ia flow acts very similarly
o the 13k shown here in an imagined position between the 20Vrms
generator output and the anode terminal.
Measurements tell us Ra = 13k for the Ea & Iadc condition in
Fig 6.
Total anode load of R3 47k // R4 100k = 32k and is seen in series
with Ra and gene to show Iac flow
around the power producing circuit in Fig 7.
Vac in 6SN7 in Fig 7.
If Vg input = 1.0Vrms, gene output = 20Vrms, which then flows in
13k and 32k to make Iac = 20V / 45k = 0.444mAac.
The anode output Va = RL x Iac = 32k x 0.444mA = 14.22Vrms.
Therefore gain between Vg and Vo = 14.22V / 1V = 14.22.
Is this correct? Gain may be calculated A = µ x RL / ( Ra + RL
) = 20 x 32k / ( 13k + 32k ) = 14.22, it is correct.
For any change to total RL, gain A can be re-calculated or worked
out by replacing 32k with any other RL and
working out different load current and Vac.
The idea of an equivalent model of a triode depends on the
imagined output of the voltage generator but 20Vrms
is nowhere to be found if we tried to measure it, unless the total
anode load was a CCS where there would be no
Ia across Ra, so the generator Vo will be equal to Va and a meter
with infinite Zin would read 20Vrms.
This seems to be absurd, but the anode still has an effect on
electron stream and Ia, and without any RLa the
Ia remains constant, and Ra is "still there".
For many ppl, the triode model is more easily understood than a
real triode. All Vac sources including the
Mains supply has a nominal Vac when no load is connected. There is
always some resistance between the
Vac Mains wall socket and the generator of the Vac. If we connect
a 3kW heater, the mains Vac might reduce
from 245Vac to 240Vac which may produce 12.5A through heater, and
the source resistance is calculated
Rsource = Vchange / Ichange = ( 245V - 240V ) / 12.5A = 5 / 12.5 =
0.4r.
All power producing circuits can be modelled with a Vac source or
generator with zero resistance, and with
an added series resistance to an output load.
If 32k RL was replaced with CCS of infinite resistance, then the
V-generator model would still make 20Vrms.
Ra of 13k would still be in series with the output terminal.
But if meter Zin was 5M0 bypassed with 1nF, at 1kHz the meter Zin
is dominated by Xc 1nF = 159k.
There is a low pass filter with 13k in series with 159k, and the
total Z of R+C = 159.5k, and if gene Vo = 20Vrms,
then Ia = 20V / 159.5k = 0.1254mA, and Vac at meter = Ia x Xc =
0.1254mA x 159k = 19.93Vac, so the Xc causes
an error of about 0.31%. This may not worry anyone, but if Ra was
65k for a 12AX7, then error becomes
7.4%, quite unacceptable. Using 100Hz Vac would be more accurate
with a digital voltmeter. But where
Ra > 100k, any digital meter tells you lies at 1kHz.
To avoid high errors with high Ra and C shunting sag, one could
use a 10:1 CRO probe with Cin < 20pF,
R divider 900k + 100k, for probe R = 1M0, but whatever is used to
measure the Vac across 100k is prone
to shunt C and R loading errors and any inaccuracy of R values in
the divider. 13k feeding 1M0 will give error
= 1.3%, and would be about 9% if Ra was 100k.
To be more accurate involves a much higher level of discipline.
One could use a well made cathode follower
buffer shown in Fig 4 with paralleled 6DJ8. Grid input Rin >
11M0, and Cin < 30pF, easy to make with a
bootstrapped 470k Rg as I show in Fig 4.
The Rout at cathode = 90r, and Vo = 0.96 x Vg input, so the exact
Vg can be calculated = Vk / 0.96.
Alternatively, the cathode resistor of about 19k have taps for
exactly 0.5 x Vg, with Rout at 8.5k, or have a
tap for 0.1 x Vg, with Rout at 1k8. This way the measurement does
not affect the voltage level to be measured.
A pentode could also be modelled. A 6AU6 with similar Ea and Ia as
for 1/2 6SN7 would have Ra = 1M5,
gm = 3mA/V, and µ might be 4,500. These are approximate figures.
Therefore the 1Vrms input would produce
an imagined 4,500Vrms across the V-generator which then feeds Ra +
RL = 1,532k so Vo is close to 94Vrms.
It is very difficult to measure Ra which is so high, and affected
by a small amount of shunt C.
The better way to determine Ra > 100k is to measure Va from a
given tube with two different RLa without
change of Ia or Ea conditions or change of input Vg. This is all
described above. For more about curves and
load lines see Basic Tube
Operation 2.
-------------------------------------------------------------------------------------------------------
Negative Feedback in Triodes.
In the Fig 6 schematic, Ea = the anode voltage minus the cathode
voltage = +140V - 5V = +135V.
The cathode is well bypassed to 0V with 470uF, so for Vac we can
consider the cathode is connected to 0V.
When we calculate resistance "looking into anode" we get R = Ea /
Ia = 135Vdc / 3.4mAdc = 39.7k.
Yet we know that when we change Ea slightly the measurement of
real resistance looking into anode 13k,
the value of Ra seen on data sheets for the Ea and Ia conditions.
What is preventing the triode from operating like a pure
resistance? If the Ea and Ia conditions were
changed to +90V & 4.4mA, Ea / Ia = 20k4, and for 200V &
2.2mA, Ea / Ia = 91k, but if we measure Ra
from test with Vac change / Ia change, we will find it remains
between about 9k and 15k, and Ra is
proportional to the slight change of gm of anode, and gm of
the grid.
We always must remember that the heat liberated by electron from
cathode to anode = Ea x Ia, and its
the same rule as for a real resistance. For Vac where there is a
constant Vdc across anode to cathode or
across a resistance, The heat remains constant where Vac is a
symmetrical sine wave and no load current
occurs. With RLa connected to a tube producing pure class A Po for
a load, the total heat to tube and load
remain constant, and tube heat reduces by the amount of Po in
load. So there is much to know about tube
equivalent resistances and load et all.
Fig 8. Current generator model for 6SN7.
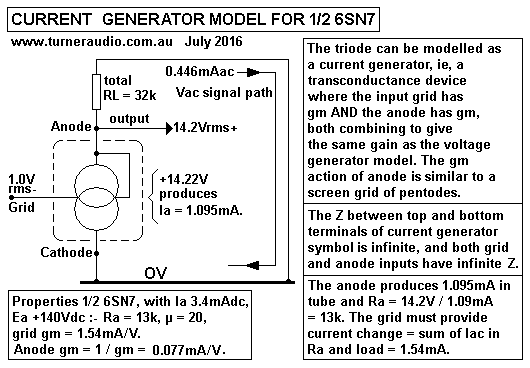
Fig 6 models the triode as a current generator.
The current gene model with two overlapping circles have top as
anode terminal and bottom as cathode.
There is infinite Z between top and bottom of circles. Grid input
is shown to left side which produces a
current change = Vg x gm. The right side shows a second input
operates like the grid and which is
equivalent to the anode's effect on Ia = Va x anode gm. The anode
gm is less than grid gm, but has
maximum effect on Ia where triode gain is highest, ie, where RLa
is a highest number of ohms.
The triode anode gm is easily calculated once Ra is known and = 1
/ Ra. Ra here = 13k,
so anode gm = 1 / 13k = 0.077mA/V. So if grid was grounded to 0V
with say 1uF, then raising Ea by +14.22V
by some external applied signal will increase Ia by 14.22V x
0.077mA/V = 1.094mA.
The grid Vg is an inverting input, and with RLa = 32k, and Va =
+14.22Vrms, Vg = -1.0Vrms. So grid -Vg
reduces Ia by -1.54mA, ie Vg x grid gM, to cause Va to go more
positive. But the positive going anode
opposes the action of grid to produce +1.094mA.
The grid Vg has to produce more current reduction than anode
produced current increase, and the resultant
current change is = -1.54mA + 1.094mA = -0.446mA, so less V across
RLa = RL x Ia = 32k x 0.0446 = +14.22Vac.
For the anode gm to work on space charge and alter the Ia with
optimal linearly, the triode should be biased for
Ea and Iadc to give a wide linear region of Va production in class
A. The triode should not be biased near cut off,
with Eg not too negative, nor be biased too close to 0V, both of
which will cause very high THD.
Anode gm and pure class A operation depends on a fixed Eg1 Vdc
from a - Vdc supply, or with a well
bypassed Rk. Without Ck bypass C, the triode has about 3dB local
current NFB in this example for 1/2 6SN7.
The current or voltage generator models can still be used, but
with unbypassed Rk between cathode terminal and 0V.
The whole operation must be re-analyzed.
Fig 8 for1/2 6SN7 shown in Fig 6 is set up in simplest way to show
only Vac and Iac operation and without DC
operation to confuse anyone. In addition to the Va = +14.22Vrms,
we can assume we would measure say 1.4%
THd, mainly 2H, and we can assign its phase, and it will be
+0.2Vrms, but let us call it +0.2Vdn.
This observed +Vdn causes Idn current by gm action = +0.2V x
0.077mA = - 0.0154mA. BUT, we have +0.2Vdn
at anode and Idn in RLa = 0.2V / 32k = 0.00625mA.
It should seem a paradox exists here because we see that the anode
gm produces more distortion current in
the opposite direction to the current measured. Just how could
this be?
Well, without anode gm, the distortion current would have been the
sum of the two currents in opposite direction.
This means without anode gm, Idn would have been 0.00625mA +
0.0154mA = 0.02165mA, and Vdn would be
+0.693Vrms. Without anode gm, the grid would have to only produce
anode current of 0.446V, so Vg would be
0.289Vrms, and gain would be 49. In other words, the THD without
anode gm = 4.87%, and all this is typical for
a small pentode with grid gm same as 6SN7.
So if there is +0.02165mA THD current without anode gm, then with
anode gm, THD current is reduced to
0.00625mA. The THD has been reduced by factor = 0.00625 / 0.02165
= 0.289 = -11dB. If this is not NFB
action, then I'll eat my hat.
The bonus is that spectral content of the triode THD is mainly 2H
and even numbered H, and better than
pentode with both even and odd number H. Without anode gm, the Ra
would be like a pentode, perhaps 1
M0, but with gm the Ra becomes 1 / gm, much lower than any
pentode.
Triode THD is minimized where there is least Ia change, and if 1/2
6SN7 has CCS Idc feed = 3.4mA, and no
other RLa, the Va max could be 63Vrms and with maybe 2% THD,
which implies THD at 0.63Vrms = 0.02%.
This is about what I have measured for SET operation in preamps.
For balanced operation with both triodes
in 6SN7 in a differential amp, THD with high value RLa may have 1%
for 2 phases of 60Vrms, and at 0.63V,
THD < 0.01%.
The THD % is somewhat difficult to calculate because Ia is
produced by a complex formula, and the experts
are still arguing 100 years after triode amps became possible, and
if experts disagree, then what chance to I
have to be certain of the mathematics. It is sufficient to simply
measure whatever you are sure to find,
knowing some general rules for setting up tubes to perform
optimally.
Va output = Ia x RL // Ra. BUT, Ia = K constant x gm x ( square
root of Vg cubed ).
This horrid formula isn't exactly correct, and Ra is not a fixed
resistor, but an active element of anode gm, and
gm varies with current. The transfer function of Vg vs Va has been
argued about endlessly and computer
simulation of triodes and pentodes has become better over the last
20 years, but from what I have seen,
the curves you measure can be different to the best curves created
by a formula with many added complex
compensations. The only way I know to make a formula work over a
wide range of Ea and Ia for a particular
tube is use the same methods used in 1955 without any PCs. But
today's world at least gives us the
opportunity to produce a 2D drawing of curves in an image file,
and more accurately than anything in
1955 using analog tube circuits to drive motors to work a pen on a
sheet of paper, all carefully calibrated,
but capable of errors of maybe 5%.
Tube makers bent over backwards to produce good data sheets for
each tube type in many thousands.
The 1955 curves for a 6SN7 will be found accurate enough today,
and today's 6SN7 production gives
the same outcome as 1955. It does take a huge effort to produce
accurate curves, all well calibrated, and
there is no enthusiasm for such effort in our digital world where
demand for vacuum tubes is low.
But we can say that a triode without its anode gm would behave
just like a pentode which has a screen grid
which has a fixed Vdc about the same as the anode Ea. The screen's
electrostatic field effect prevents
nearly all the anode field having any gm effect on the electron
stream. The pentode THD is somewhat difficult
to predict. But wherever its screen is connected to anode for
triode operation, the same Vac below 20Vrms
has less THD for the same RL.
Power triodes for power for transmitters and industrial uses have
always been large and expensive.
But the ordinary man has never had to buy one, because for most of
1920s a low power audio triode was
included in the early radios which used only triode RF amps. Horn
loaded speakers with limited F
response could make adequate listening levels with 1/2 a Watt.
These had maybe 25% efficiency in class A.
Type 45, then 2A3 became the best to be had for audio power amps,
and a PP pair of 2A3 could make 10W
in class AB1; this was a luxurious amount of power for the very
few rich ppl. By 1930, triode signal tubes
were replaced by pentodes in superhet AM radios for RF and IF
amps. Multi-grid hexodes or octodes
or triode-hexodes were used for frequency converters. Triode
output tubes were replaced by power pentodes.
By 1935, the triode was used far less often, a mainstream trend
which went on until 1960 when transistors
had ppl putting their old tube amps and radios into the rubbish
bin because they found they just must have
two channels for the new stereo sound from LPs, and the guys at
the shop had these cool systems with
transistors and even the missus agreed to have such rubbish in the
house. Have you ever heard an average
sound system of 1960? It is an insult to ears, music and our
brains, and to the great composers of good music.
It was cheap and nasty, but then most who could afford such
garbage had 3 kids and were always trying to avoid
costs of all things.
For power amps, triodes have a restriction to Va negative swing
because the load line intersects the Ra curve
for Eg = 0V. The power triode grids must be pushed hard with class
AB2 operation to get the efficiency to a
maximum of 60%.
However, despite so many triode shortcomings, they remained king
in the minds of audiophiles.
There were discussions in early 1930s by many scholars about all
aspects of tube construction, materials and
behavior. A Mr Terman wrote books about use of tubes in radio
transmitters, receivers, industrial amplifiers,
and 101 other applications. In one of Terman's books a Professor
Child wrote about the "self - regulation" of anode
current in triodes. It is difficult to read because we are not
familiar with the terms used, and the mathematics
used to describe tube operation are baffling. But let us be sure
to respect greater minds of those who
preceded us, because so often they knew more than we do.
From a simple man's point of view, I see the current generator
model best explains all class A tube behavior at low levels.
----------------------------------------------------------------------------------------------------------------
Pentodes and beam tetrodes.
It is appropriate to illustrate that although there is NFB in
triodes, there is virtually no NFB operating within
pentodes and beam tetrodes.
Long ago in about 1921, It may have been Philips who placed a
second grid between the control grid g1 and
the anode using similar wire structure for the g1 helical winding.
This was the screen grid, g2, and it was
usually connected to a fixed positive Vdc, Eg2, slightly less than
Ea. The resulting tube was a tetrode.
This caused the anode voltage change to have very little field
effect on the space charge and cathode to anode
electron current flow so Ra became very high while grid gm stayed
the same.
Now for all tubes, µ = gm x Ra. Tetrode µ could be
thousands rather than the maximum of about 100 as it is
in a 12AX7, because Ra could be megohms and not say 65k max like a
12AX7.
But the 1922 tetrode had some really strange secondary emission
effects where Ea was low, with Eg2 close to Ea,
and electrons which bounced off the anode could then be attracted
to screen, making the low Ea region of
operation unusable. So the pure 4 electrode tetrode wasn't much
used and is never used now. But later in 1920s
Philips engineers added a third grid, g3 between the anode and
screen g2, with wires having course pitch and
this was kept at cathode potential and prevented electrons
bouncing from anode to get to screen g2. THEN
the pentode matured to be an extraordinary device which allowed
huge advances in radio transmission and
reception at high frequencies.
The main reason pentodes work well at high F is their lack of
anode gm, ie, lack of internal NFB. Thus their gain
is much higher so instead of 2 feeble triodes, you could have one
pentode with almost no extra cost. Nobody cared
much about the increase in THD and IMD.
In all tubes, there is capacitance between electrodes. In a small
signal triode like 12AX7, the C between grid and
cathode < 10pF. And between grid and anode, there is about 3pF,
a very small amount of C. But a typical 12AX7 has
gain = 70, and when Vg = +0.1V, the Va = -7V. The Vac across the
3pF then effectively becomes 3pF x 70 = 201pF.
Instead of grid Zin remaining over 1M0 at LF, at 10kHz, grid Zin =
72k, and at 1Mhz the Zin has become 722r,
which has a shunting effect for whatever is driving a 12AX7. So
this triode like many others is useless for common
cathode gain stages at high F.
The C which reduces gain at HF is called the Miller Capacitance. A
Mr Miller must have been the first man to work
this out.
In a pentode with a fixed Eg2, the capacitance between anode and
grid is interrupted. Whatever is feeding grid g1
is loaded by static C between grid and cathode and between grid
and screen, a total of say 10pF so that getting
a pentode to perform at up to say 120MHz is possible, with high gm
pentodes like 6EH7. But 2MHz is easy for
AM radio with low gm pentodes like 6U7. The C between screen g2
and anode is low and has little effect in
upsetting tuned LC circuits.
Neutralization is a technique needed in RF triode power amps to
apply a positive FB signal to cancel the Miller C.
It is a sometimes tricky thing to do, and bad adjustment of the
neutralization C easily leads to oscillations.
Pentodes give far fewer problems of stability at HF.
Audiophiles lamented the development of pentodes which they saw as
much inferior devices for all small
signal amps. The power pentodes and the power beam tetrodes
developed in 1930s were also loathed by
many who believed the 2A3 or 300B was superior to everything else.
Triode connection of pentodes and
power beam tetrodes became common, and then audiophiles had very
little to complain about.
The famous 1947 12W class A PP amp designed by Mr D.T.N Williamson
used a pair of KT66 with screens
tied to anodes to have them operate as triodes. This 1947 made
0.1% THD at 12W, and used 20dB GNFB
and used 2 x 6SN7 for the input and driver stages; it was all
triodes, and bandwidth from 20Hz to 75kHz, and
well restored samples sound every bit as good as any other 12W amp
now made.
Arguments still rage about triodes versus pentodes for audio. But
no two audiophiles ever agree about more
than 3 issues out of 10.
Fig 9.
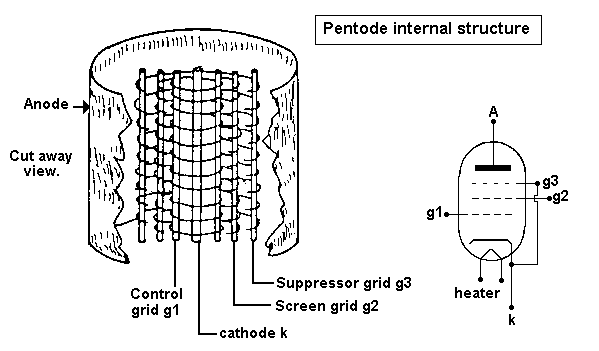
Fig 9 has basic construction and pentode schematic. The extra grid
g3 was called the suppressor grid because it placed
a 0V electrostatic field between the anode and screen to prevent
electrons bouncing off the anode and being absorbed
by the screen when the anode voltage swung to a lower voltage than
the screen.
Fig 10. 6AU6 pentode operation.
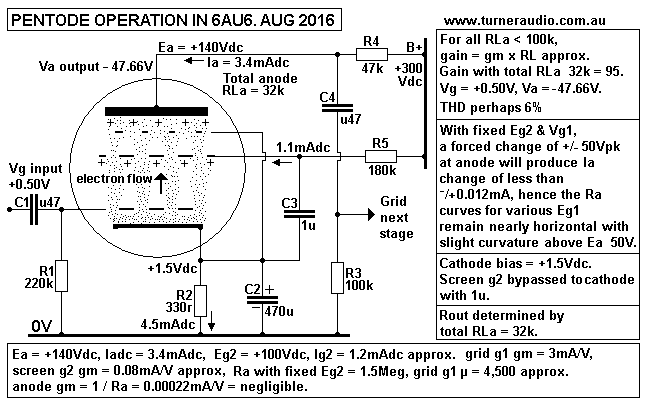
Electrons in the space charge around the cathode are controlled by
the electrostatic fields of control grid g1 and
screen grid g2. In pentode operation, the g2 is bypassed to
cathode with 1uF so there is no Vg2 between g2 and
cathode. Therefore g2 has no control over Iac. Electrons which get
past the grid are mainly attracted by the fixed
positive voltage of g2. Between 1/3 and 1/4 of these electrons are
absorbed by screen wires which produce a screen
Idc flow shown here as 1.1mAdc. Most electrons get past the g2 to
head for the anode.
The grid and screen wires are aligned to give the electrons a best
chance of proceeding to anode without too may
being absorbed by g2. The suppressor grid g3 prevent "secondary
emission", ie, the electrons bouncing off anode
when Ea is low, and then returning to the fixed and higher Eg2.
In beam power tetrodes, also called beam power pentodes, there is
no suppressor grid, but instead there are two
beam forming plates between g2 and anode which are both at cathode
potential which cajole electrons into a
beam towards anode so that their negative charge repels electrons
bouncing off anode to return to anode.
These beam former plates are permanently connected to cathode
within the tube. Most power beam tetrodes,
have screen Idc less than 12% of anode Idc, and much less than
EL34. Pentodes have g2 Idc up to 1/3 of anode Idc.
The input impedance to screen g2 is fairly high where it is used
to apply Vac from the anode where triode
connection is used, or from some other source of Vac. The screen
Zin is affected by Vac at anode.
G3 has very little Idc flow and has high Zin for Vac. It is seldom
used for Iac control and used mainly to stop
secondary emission with a local fixed low voltage field by
connection to cathode. But sometimes g3 is used
for much greater Iac control in oscillators; the 6DT6 was made to
deliberately to allow g3 Ia control with g1,
and that was used in countless audio detectors in FM radios and TV
sets.
Suppressor g3 are sometimes internally connected to cathode, eg,
in EL84, but in many other pentodes such
as EL34, 6AU6, 6BX6, it is brought out to a pin for a variety of
control functions. Most pentodes in AF and RF
amps have g3 connected to cathode at tube socket.
In much equipment made in the 1950s and 1960s, pentodes such as
the 6AU6 with mini 7 pin bases and
EF86 with 9 pin bases were favored in countless audio circuits
because they gave more circuit gain than
triodes which allowed more external loop NFB to keep the gain of
multiple channels equal, and keep noise
& distortion & output resistance low, and all without such
a large and expensive number of tubes.
The power pentode or beam tetrode is best set up as a class A
single tube with the fixed Eg2 at about 2/3 of Ea.
However, it is wise to adjust Eg2 to be the lowest value which
still allows the maximum Va swing at lowest THD
for the range of RLa loads to be used.
Pentodes and beam tetrodes are often used as triodes with g2 and
g3 connected to anode for "triode strapping",
ie, triode operation which then allows all the Va to applied to
g2, and thus the screen acts with gm / Ra of the
triode thus formed.
6AU6 has g2 gm = 0.08mA/V approximately. With g2 connected to
anode, the anode and g2 become ONE
electrode; both form the anode, and they have combined gm equal to
the screen acting in its own, ie, 0.08mA/V.
Thus a 6AU6 will have anode gm = 0.08mA/V, and its Ra = 1/ gm =
12.5k, and the µ = g1 gm x Ra = 3.0 x 12.5 =
37.5. The gain for total RLa = 32k = 27, and less than 1/3 of
pentode gain. But the THD is much lower for Va say
20Vrms, and the spectrum of THD has less odd H, and sound is
better.
A pentode can make good CCS constant current sink for a pair of
commoned cathodes in a long tail pair in a
differential amp. Few now would do this because a single bjt such
as MJE340 will work better as a passive
constant current sink. And where a pentode has its cathode at say
-150Vdc, the heater should also have
a -Vdc bias which may require yet another 6.3Vac winding just for
this tube.
A pentode can also make a CSS constant current source between B+
of say +300V and the anode of a triode
gain tube such as 1/2 6SN7 or 6CG7 with its Ea = say +150Vdc. The
pentode heater will require a +Vdc bias.
A 6AU6 or 6BX6 will work well to make a CSS with finite RLa of 3M0
at least, and with its cathode being a low
Rout terminal if needed. This then forms a µ-follower gain stage
which can be argued to be better than µ-follower
with two medium µ triodes such as 12AU7 which I found to be
superlative in my 10
tube triode preamp.
The very high Ra of pentodes and lack of internal electrostatic
NFB, ie, anode gm, and the low Miller input C
makes pentodes work well at RF. I found I could make a Wien bridge
oscillator full of pentodes with maximum
oscillator F at 2.2MHz.
The pentode produces much more THD for the same Va than if triode
connected, or compared to other triodes with
similar g1 gm. Pentode THD contains a more complex array of odd
and even number H which vary with the load value,
and the phase of the H may be reversed between low RLa and high
RLa. To reduce all this, NFB must be used.
If say 10dB of NFB is delivered with a shunt NFB network of 2
resistors for 6AU6 in Fig 10, gain is reduced to about
the same as triode, and so is THD. But triode THD spectrum is
still better than the pentode with 10dB loop NFB.
The input Rin to a shunt NFB network is always lower than grid
input bias Rg. So what is really the benefit of using
pentodes in signal amps where there is no concern about costs
which trouble manufacturers?
I have never seen any reason to use a pentode in any preamp except
for where I used a 6EJ7 connected as a triode
to be cathode driven by a j-fet 2SK369 in cascode for a phono
input stage in my 10 tube triode preamp.
I have used pentodes like EL84 strapped as triodes to drive output
tubes, as I show in 8585
and 300W
amps.
The EL84, EL86, EL34 make excellent triode drivers with low Ra and
with triode µ of 20, 10, and 9 respectively.
But other applications beckon where the screen g2 is used as a NFB
port to drive a following amp stage which is
a cathode follower or mosfet source follower of an output stage.
Thus the pentode works to produce Va say
40Vac to drive grids or gates of a following output stage which
makes Vout from cathodes or sources = say 35Vac.
The pentode g2 is bypassed to the output stage 35Vac, and includes
the pentode THD and any THD of output
devices and it is all reduced by the gain of the screen g2 if
using a high value RLa which is a choke + R in series.
See the example at schematic for a single EL34 driving mosfet
source followers at my page on hybrid amps.
For EL34, EL84, EL86, and EL36, the screen has a usefully high g2
gm above
0.4mA/V, much more than for a 6AU6 with g2 gm 0f 0.08 approx.
Fig 11.
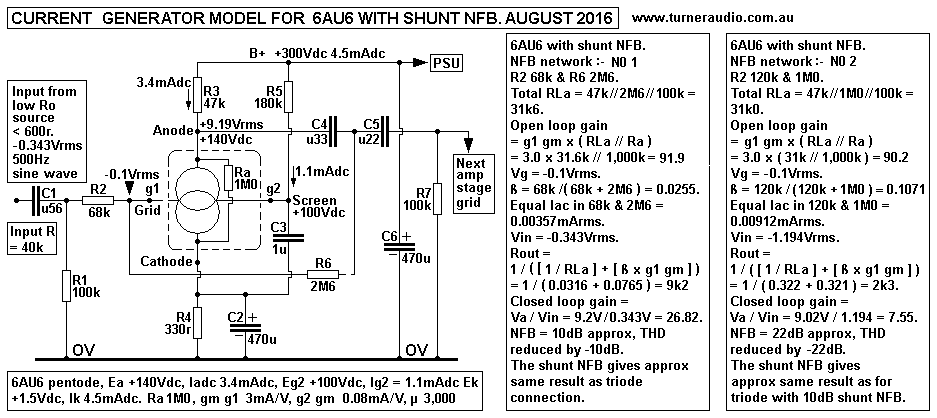
Fig 11 shows a 6AU6 modelled as a current generator with TWO
inputs, grid g1 with Zin > 1M0, and screen g2
with Zin > 50k.
The screen g2 is bypassed to cathode which is bypassed to 0V so no
Vac appears at g2.
The Ra of 6AU6 is a nominal figure which is difficult to determine
using a ruler and pencil on data sheets, and the
Ra line curvature shows some variation on each line for various
Eg1 bias -V, The Ra we need to know is at the idle
Q point for Ea +140V and Ia 3.4mAdc, and for a small swing of Ea.
For most pentodes and beam tetrodes the Ra is a higher for low Ia
and lower for high Ia. It is NOT a constant value,
and nor is the g1 gm and g2 gm which vary with Ia. The Ra is shown
in model as Ra = 1M0 as across the generator.
Regardless of whether the pentode is pentode connected as shown or
triode connected ( not shown ), the anode
still has some gm effect on Ia flow = 1 / Ra = 1 / 1M0 =
0.001mA/V, a tiny amount which most ppl just ignore.
If the 6AU6 were to have a CCS Idc feed of 3.4mAdc, and its finite
R = 5M0, and no other loading from NFB network
of grid bias Rg, then gain g1 gm x ( 1M0 // 5M0 )
= 3.0 x 833k = 2,499, an astonishing result from a single humble
tube.
Its also a little impractical to ever expect such high gain, and
if circuit and tube shunt C = 20pF, the F2 pole is at 9.5kHz.
Tube samples would vary so much nobody could depend on this high
gain. Noise may be a problem. Usually, the gain
of a pentode is limited by practical values for total RLa. In many
circuits I have seen 6AU6 and other signal pentodes
such as EF86 used with 180k RLdc, and total RLa = 120k, and gain =
100 so gm = 0.8mA/V.
This is seen in Quad II power amps.
Here I have RLdc only 47k, for higher Ia which raises the gm, and
with total RLa of 31k, gain > 90. It may be argued
long and hard that the higher Ia, gm and lower RLa gives better
sound than for lower Ia, gm and higher RLa.
What we do know is that manufacturers were allergic to high
currents in anything because their production meant
higher power supply costs!
Two different NFB networks are shown in the 6AU6 pentode model. No
1 has 11dB NFB which changes pentode
operation to near the operation of triode connection. No 2 has
22dB NFB and could be used as a practical line stage
preamp. Notice that the the tube gain is affected by the loading
effect of NFB network resistance. This is quite OK,
and if switchable gain selection was required, the R6 could be 6
switched resistors of 2M7, 1M5, 1M0, 680k, 470k, 220k.
Where the output Va < 5Vrms, the performance will be faultless.
Readers should now move to Loadline Analysis for small signal
tubes in Tube
Operation 2
To Tube
operation 3
To tube
operation 4
To Index Page







