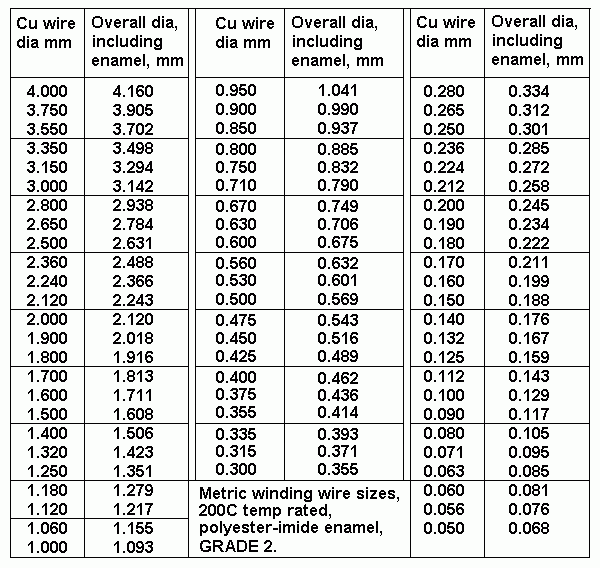
| 0W to 15W |
Total P layers |
Primary and Secondary
layer distribution. |
P+S section pattern |
| 0 to 7W |
10p to 24p |
S - 10p~24p - S |
2S + 1P |
| 7W - 15W | 10p to 20p | S - 5p~10p - S - 5p~10p - S | 3S + 2P |
| 7W - 15W |
10 to 20 | 2p~4p - S - 4p~8p - S - 4p~8p - S - 2p~4p | 3S + 4P |
| 7W - 15W |
10 to 20 |
S - 4p~6p - S - 4p~6p - S - 4p~6p - S |
4S + 3P |
| 15W to 30W |
Total P layers |
Primary and Secondary
layer distribution. |
P+S section pattern |
| 12p | 2p - S - 4p - S - 4p - S - 2p | 3S + 4P | |
| 12p | S - 4p - S - 4p - S - 4p - S | 4S + 3P | |
| 13p |
2p - S - 3p - S - 3p - S - 3p - S - 2p | 4S + 5P |
|
| 14p | 2p - S - 3p - S - 4p - S - 3p - S - 2p | 3S + 4P | |
| 14p | S - 5p - S - 4p - S - 5p - S | 4S + 3P | |
| 15p |
S - 5p - S - 5p - S - 5p - S | 4S + 3P |
|
| 15p |
2p - S - 4p - S - 3p - S - 4p - S - 2p |
4S + 5P |
|
| 16p | 3p - S - 5p - S - 5p - S - 3p | 3S + 4P | |
| 16p | S - 4p - S - 4p - S - 4p - S - 4p - S | 5S + 4P | |
| 16p | 2p - S - 4p - S - 4p - S - 4p - S - 2p | 4S + 5P | |
| 18p | 3p - S - 6p - S - 6p - S - 3p | 3S + 4P | |
| 18p | S - 4p - S - 5p - S - 5p - S - 4p - S | 5S + 4P | |
| 20p | 3p - S - 7p - S - 7p - S - 3p | 4S + 3P | |
| 20p | S - 5p - S - 5p - S - 5p - S - 5p - S | 5S + 4P | |
| 20p | 2p - S - 5p - S - 6p - S - 5p - S - 2p | 4S + 5P |
| 30W to 100W |
Total P layers |
Primary and Secondary
layer distribution. |
P+S section pattern |
| 11p |
S - 4p - S - 5p - S - 4p - S |
4S + 3P |
|
| 11p |
2p - S - 2p - S - 3p - S -2p - S - 2p
|
4S + 5P |
|
| 12p |
S - 4p - S - 4p - S - 4p - S | 4S + 3P |
|
| 12p |
2p - S - 3p - S - 2p - S - 3p - S - 2p
|
4S + 5P |
|
| 13p |
S - 4p - S - 5p - S - 4p - S | 4S + 3P |
|
| 13p |
2p - S - 3p - S - 3p - S - 3p - S - 2p | 4S + 5P |
|
| 14p |
S - 5p - S - 4p - S - 5p - S |
4S + 3P |
|
| |
14p | S - 3p - S - 4p - S - 4p - S - 3p - S | 5S + 4P |
| 14p |
2p - S - 3p - S - 4p - S - 3p - S - 2p | 4S + 5P | |
| 15p |
S - 5p - S - 5p - S - 5p - S | 4S + 3P |
|
| 15p |
2p - S - 4p - S - 3p - S - 4p - S - 2p | 4S + 5P |
|
| 16p |
S - 5p - S - 6p - S - 5p - S |
4S + 3P |
|
| 16p |
S - 4p - S - 4p - S - 4p - S - 4p - S | 5S + 4P | |
| 16p | 2p - S - 4p - S - 4p - S - 4p - S - 2p | 4S + 5P | |
| 18p | S - 4p - S - 5p - S -
5p - S - 4p - S |
5S + 4P | |
| 18p |
2p - S - 5p - S - 4p - S - 5p - S - 2p | 4S + 5P | |
| 19p |
2p - S - 5p - S - 5p - S - 5p - S - 2p | 4S + 5P |
|
| 20 p | S - 5p - S - 5p - S - 5p - S - 5p - S | 5S + 4P | |
| 20p |
2p - S - 5p - S - 6p -
S - 5p - S - 2p |
4S + 5P | |
| 21p |
3p - S - 5p - S - 5p - S - 5p - S - 3p | 4S + 5P |
|
| 22 p | S - 5p - S - 6p - S -
6p - S - 5p - S |
5S + 4P | |
| 22p |
2p - S - 6p - S - 6p - S - 6p - S - 2p | 4S + 5P |
| 100W to 250W |
Total P layers |
Primary and Secondary
layer distribution. |
P&S section pattern |
| |
10p | 2p - S - 2p - S - 2p - S - 2p - S - 2p | 4S + 5P |
| 10p | S - 2p - S - 3p - S - 3p - S - 2p - S | 5S + 4P | |
| 10p | 1p - S - 2p - S - 2p - S - 2p - S - 2p - S - 1p | 5S + 6P | |
| 10p | S - 2p - S - 2p - S - 2p - S - 2p - S - 2p - S | 6S + 5P | |
| 12p | 2p - S - 3p - S - 2p - S - 3p - S - 2p | 4S + 5P | |
| 12p | S - 3p - S - 3p - S - 3p - S - 3p - S | 5S + 4P | |
| 12p | 1p - S - 2p - S - 3p - S - 3p - S - 2p - S - 1p | 5S + 6P | |
| 12p | S - 2p - S - 3p - S - 2p - S - 3p - S - 2p - S | 6S + 5P | |
| 12p |
S - 2p - S - 2p - S - 4p - S - 2p - S - 2p - S | 6S + 5P | |
| 13p |
2p - S - 3p - S - 3p - S - 3p - S - 2p | 4S + 5P |
|
| 13p |
S - 3p - S - 4p - S - 3p - S - 3p - S | 5S + 4P |
|
| 13p |
S - 2p - S - 3p - S - 3p - S - 3p - S - 2p - S | 6S + 5P |
|
| 14p |
2p - S - 3p - S - 4p - S - 3p - S - 2p | 5S + 5P | |
| 14p | S - 3p - S - 4p - S - 4p - S - 3p - S | 5S + 4P | |
| 14p | 1p - S - 3p - S - 3p - S - 3p - S - 3p - S - 1p | 5S + 6P | |
| 14p | S - 2p - S - 3p - S - 4p - S - 3p - S - 2p - S | 6S + 5P | |
| 16p | 2p - S - 4p - S - 4p -
S - 4p - S - 2p |
4S + 5P | |
| 16p | S - 4p - S - 4p - S - 4p - S - 4p - S | 5S + 4P | |
| 16p | 2p - S - 3p - S - 3p - S - 3p - S - 3p - S - 2p | 5S + 6P | |
| 16p | S - 3p - S - 3p - S -
4p - S - 3p - S - 3p - S |
6S + 5P | |
| 18p | 2p - S - 5p - S - 4p -
S - 5p - S - 2p |
4S + 5P | |
| 18p | S - 5p - S - 4p - S -
4p - S - 5p - S |
5S + 4P | |
| 18p | 2p - S - 4p - S - 3p - S - 3p - S - 4p - S - 2p | 5S + 6P | |
| 18p | S - 3p - S - 4p - S - 4p - S - 4p - S - 3p - S | 6S + 5P | |
| 19p |
S - 3p - S - 4p - S - 5p - S - 4p - S - 3p - S | 6S + 5P |
|
| 20p | 3p - S - 5p - S - 4p - S - 5p - S - 3p | 4S + 5P | |
| 20p | S - 5p - S - 5p - S - 5p - S - 5p - S | 5S + 4P | |
| 20p | 2p - S - 4p - S - 4p - S - 4p - S - 4p - S - 2p | 5S + 6P | |
| 20p | S - 4p - S - 4p - S -
4p - S - 4p - S - 4p - S |
6S + 5P | |
| 21p |
S - 4p - S - 4p - S - 5p - S - 4p - S - 4p - S | 6S + 5P |
|
| 21p |
3p - S - 5p - S - 4p - S - 5p - S - 3p | 4S + 5P |
|
| 22p | 3p - S - 5p - S - 6p - S - 5p - S - 3p | 4S + 5P | |
| 22p | S - 5p - S - 6p - S - 6p - S - 5p - S | 5S + 4P | |
| 22p | 2p - S - 5p - S - 4p -
S - 4p - S - 5p - S - 2p |
5S + 6P | |
| 22p | S - 4p - S - 6p - S -
4p - S - 6p - S - 4p - S |
6S + 5P |
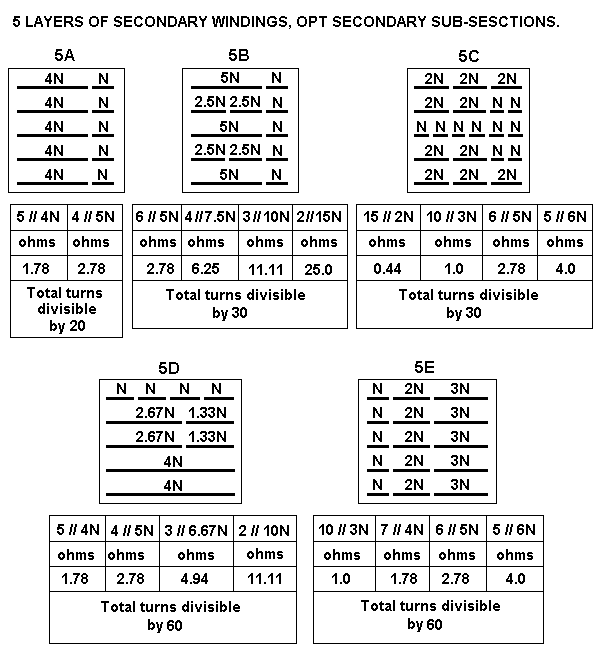
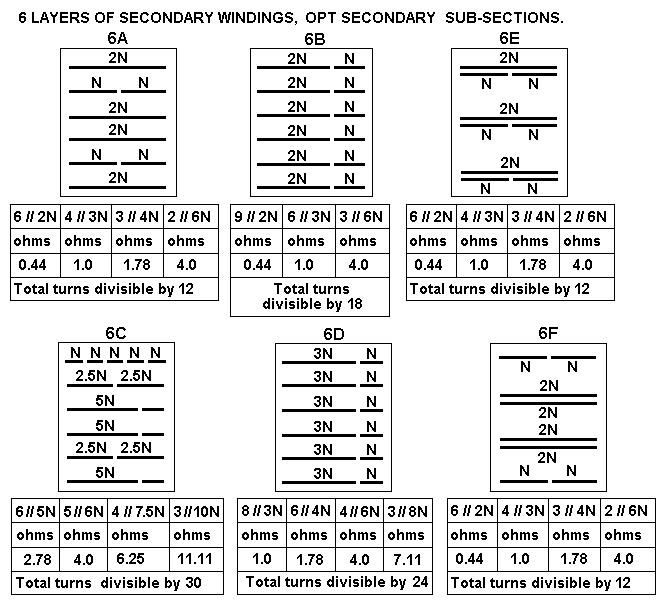
| 35W | 15p |
S - 5p - S - 5p - S - 5p - S | 4S + 3P |
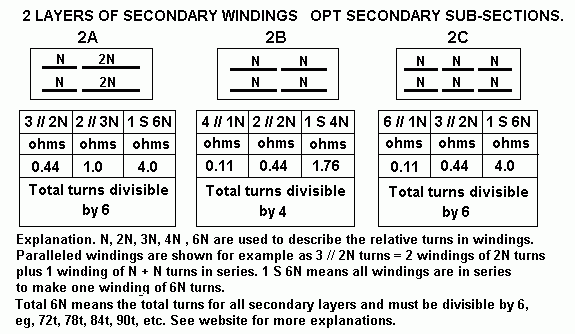
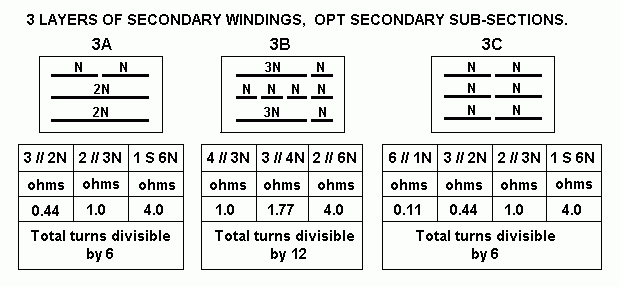
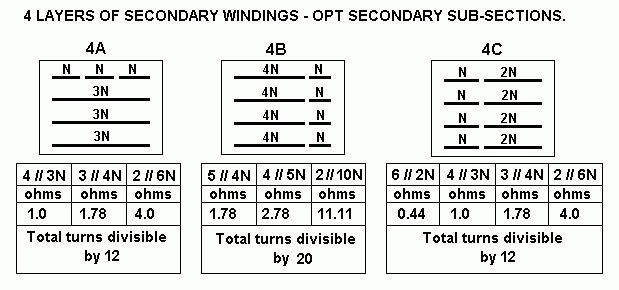

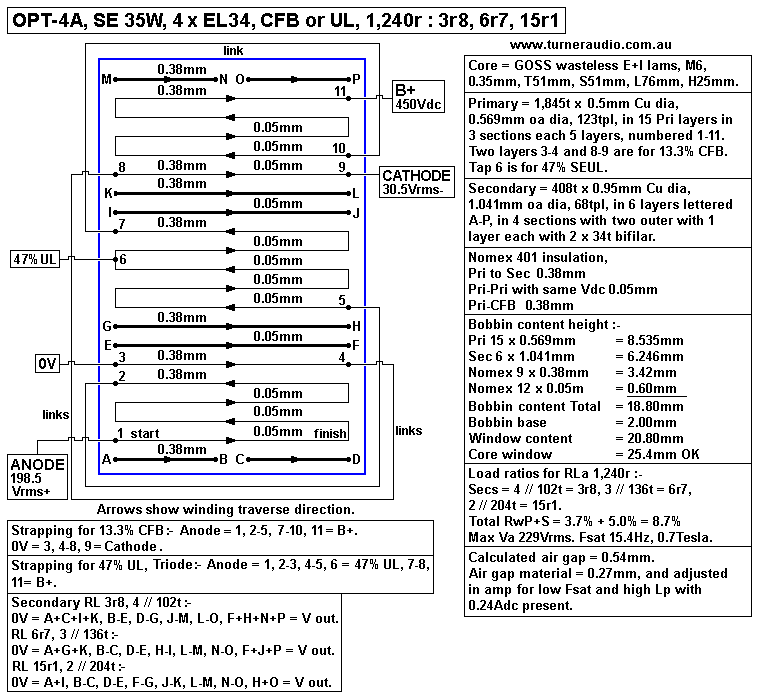
| P-S Csh at each interface, pF |
winding position |
Fraction |
Fraction Squared Factor |
Effective C at anode, pF |
| 1,037 |
14.5 / 15 |
0.966 |
0.934 |
969 |
| 1,037 | 10.5 / 15 |
0.700 |
0.49 |
508 |
| 1,037 | 9.5 / 15 |
0.633 |
0.401 |
416 |
| 1,037 | 5.5 / 15 |
0.367 |
0.134 |
139 |
| 1,037 | 4.5 / 15 |
0.300 |
0.090 |
94 |
| 1,037 | 0.5 / 15 |
0.033 | 0.001 |
1.1 |
| Total Sum 6,222pF |
2,127pF |
| Fsat |
9Hz |
12Hz |
15Hz |
19Hz |
24Hz |
| Applied Vrms |
230V |
230V |
230V |
230V |
230V |
| Bac max |
1.13T |
0.85T |
0.70T |
0.55T |
0.44T |
| Bdc |
0.27T |
0.55T |
0.70T |
0.85T |
0.96T |
| µe |
116 |
235 |
300 |
364 |
411 |
| Air gap |
very big |
big |
correct? |
small |
very small |
| Lp |
5.4H |
11H |
14H |
17H |
19H |
| XLp |
305r |
829r |
1,320r |
2,028r |
2,868r |
| Max amp Vrms No RL |
53V |
144V |
230V |
230V |
230V |
| XLp = 1,240r at |
37Hz |
17.9Hz |
14.1Hz |
11.6Hz |
10.4Hz |
| XLp // 1,240r |
296r |
690r |
880r |
1,058r |
1,138r |
| Max amp Vo for low THD |
52V |
120V |
152V |
183V |
228V |
| 1 | 2 | 3 |
4 |
5 | 6 |
7 |
8 |
9 |
10 |
11 |
12 | 13 |
14 |
| Core Tmm x Smm |
AFe sq.mm |
RLa |
Anode Power W Fsat 14Hz |
Pri Cu dia mm |
Pri oa dia mm |
Pri area 0.28 x L x H |
Np turns t |
Va Vrms 14Hz 0.7 Tesla |
Idc mA dc |
Square Afe Eqtn Factor 14Hz |
E&I Core Weight Kg |
L
x H mm area sq. mm |
Po Sec, Rw loss 10% |
| 51 x 102 51 x 76 51 x 63 51 x 51# 51 x 51 51 x 38 51 x 32 |
5,202 3,876 3,213 2,601 2,601 1,938 1,632 |
1k0 1k0 1k2 10k3 1k1 1k5 1k4 |
108.0W 68.0W 50.7W 32.9W 35.7W 20.4W 15.2W |
0.56 0.53 0.50 0.28 0.50 0.45 0.45 |
0.632 0.601 0.569 0334 0.569 0.516 0.516 |
541 541 541 541 541 541 541 |
1,355 1,500 1,670 4,850 1,670 1,930 1,930 |
324 267 247 580 200 172 145 |
475 362 292 81 254 170 150 |
500 470 450 455 435* 430 420 |
12.2 9.0 7.5 6.1 6.1 4.5 3.8 |
76
x 25 = 1,900 |
97.0W 61.0W 45.6W 29.6W 32.1W 18.3W 13.7W |
| 44 x 76 44 x 76 44 x 63# 44 x 63 44 x 63 44 x 44 44 x 35 |
3,344 3,344 2,772 2,772 2,772 1,936 1,540 |
940r 1k4 12k3 1k3 1k6 1k8 2k1 |
41.4W 40.7W 27.6W 30.0W 30.0W 17.3W 11.2W |
0.50 0.45 0.25 0.45 0.425 0.40 0.375 |
0.569 0.516 0.301 0.516 0.489 0.462 0.436 |
414 414 414 414 414 414 414 |
1,280 1,555 4,570 1,555 1,730 1,940 2,180 |
197 239 582 198 220 172 154 |
298 241 69 216 197 139 104 |
520 525 525 505 505 465* 460 |
7.8 7.8 5.6 5.6 5.6 3.9 3.1 |
66
x 22 = 1,452 |
37.3W 36.6W 24.8W 27.0W 27.0W 15.6W 10.0W |
| 38 x 76 38 x 63 38 x 51 38 x 38 38 x 25 |
2,888 2,394 1,938 1,444 950 |
2k4 2k7 3k8 3k4 4k6 |
22.8W 17.3W 12.3W 9.0W 8.0W |
0.355 0.335 0.30 0.28 0.25 |
0.414 0.393 0.355 0.334 0.301 |
305 305 305 305 305 |
1,780 1,975 2,420 2,730 3,360 |
234 217 215 174 190 |
138 113 81 74 60 |
605 575 555 485* 335 |
5.0 4.2 3.4 2.5 1.7 |
57 x 19 = 1,083 |
20.5W 15.6W 11.0W 8.1W 7.2W |
| 32 x 76 32 x 63 32 x 51 32 x 38 32 x 32 |
2,432 2,016 1,632 1,216 1,024 |
3k0 2k0 2k6 3k2 4k7 |
12.1W 14.8W 10.0W 5.0W 3.7W |
0.30 0.28 0.265 0.25 0.224 |
0.355 0.334 0.312 0.301 0.272 |
215 215 215 215 215 |
1,710 1,930 2,210 2,370 2,910 |
190 172 160 127 132 |
169 122 89 56 40 |
530 525 515 545 530* |
3.6 3.0 2.4 1.8 1.5 |
48
x 16 = 768 |
10.9W 13.3W 9.0W 4.5W 3.3W |
| 28 x 76 28 x 76 28 x 51 28 x 38 28 x 28 |
2,128 2,128 1,428 1,064 784 |
2k8 6k6 3k5 4k8 9k5 |
5.9W 7.2W 4.1W 2.5W 1.5W |
0.30 0.224 0.25 0.224 0.18 |
0.355 0.272 0.301 0.272 0.222 |
165 165 165 165 165 |
1,310 2,230 1,820 2,320 3,350 |
129 218 120 109 121 |
105 59 49 32 18 |
876 810 700 675 640* |
2.3 2.3 1.8 1.4 1.0 |
42
x 14 = 588 |
5.3W 6.5W 3.7W 2.2W 1.3W |
| 25 x 76 25 x 51 25 x 38 25 x 25 |
1,900 1,275 950 625 |
8k0 9k5 10k3 14k0 |
4.8W 2.7W 1.7W 0.8W |
0.20 0.18 0.17 0.15 |
0.245 0.222 0.211 0.188 |
135 135 135 135 |
2,250 2,740 3,030 3,820 |
196 160 133 104 |
44 24 23 11 |
870 775 730 715* |
2.2 1.4 1.1 0.72 |
38
x 12.5 = 475 |
4.3W 2.4W 1.5W 0.7W |
| 1 SxT | 2 Afe |
3 RLa |
4 Poa |
5 Cud |
6 oad |
7 Ap |
8 Np |
9 Va |
10 Idc | 11 Fact |
12 Kg |
13 LxH |
